APPENDIX I
THE GOLDEN SECTION
or
THE EXTREME AND MEAN RATIO
Among the many relationships that exist between numbers, there are some that
may be expressed as ratios and proportions. Thus when we say
that the ratio of 3 to 12 is the same as the ratio of 12 to 48, we are recognizing
the fact that there are 4 threes in 12, and that there are also 4 twelve's in
48. This may be written in the form of a proportion, thus:
The numbers 3 and 48 are known as the extremes, and the number 12 is known
as the mean. This may also be written in a fractional form:
The relationship becomes obvious when we
reduce the fractions to ¼.
This is the simplest type of proportion
because only three quantities appear: 3, 12 and 48, and it will serve our purposes
adequately.
It is a property of all such proportions
that the product of the extremes is equal to the square of the mean. Thus,
we would find that the area of a square that is 12 inches on a side is equal
to the area of a rectangle that is 3 inches wide and 48 inches long. Each would
have an area of 144 square inches.
A proportion of this kind may be written algebraically by the use of the letters
a, b, and c, thus:
a : b = b : c and a x c = b²
We may now develop a sequence of numbers based upon this pattern: 3, 12, 48,
192, 768, and so on, by simply multiplying each term by 4. Such a sequence
of numbers is known as a geometrical progression, with a constant ratio between
any two adjacent terms. In this instance the ratio is 1 : 4.
Another kind of numerical series is generated
by a process of addition, wherein the series increases by a fixed increment.
This is known as an arithmetical series. A good example of this is seen in
the column of a calendar. Take the column which reads 4, 11, 18, 25, wherein
each term is merely the previous term increased by 7. Here there is no fixed
ratio between any two adjacent terms. Thus, we cannot say that 4 : 11 as 11
: 18, nor as 18 : 25.
Now we are in search of a series of numbers
which will combine the properties of the arithmetical series with the geometrical
progression. We shall reach a halfway point in our search if we consider the
so-called Fibonacci Series, named after its discoverer, an Italian mathematician
who was born about 1180 AD. This series starts with 0, and the second term
is 1. Thereafter, each term is the sum of the two preceding terms, thus:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, etc., etc.
This series of numbers has a remarkable property, for while there is not a
fixed ratio between the terms, nevertheless if we take them two at a time, starting
them as fractions, and find their decimal values, we shall discover that these
values come closer and closer to a certain number, already familiar to the readers
of this book. Carried to six significant figures, this number is .618034…
Actually, it is an indeterminate decimal, and for most purposes it is sufficient
to carry it to three significant places only, as has been done throughout this
book.
Let us now make a table of fractions taken from the Fibonacci Series. The
(+) and the (-) signs indicate that the value is either above or below the decimal
.618034; but notice that these values converge more and more closely to that
figure as the process is carried on. Actually, the final value is reached only
when this series is carried to infinity:
| 1/1 |
|
1.000 + |
| 1/2 |
|
.500 - |
| 2/3 |
|
.666 + |
| 3/5 |
|
.600 - |
| 5/8 |
|
.625 + |
| 8/13 |
|
.615 - |
| 13/21 |
|
.619 + |
| 21/34 |
|
.618 - |
Figure 22 shows a graph of these values. Note the bold line indicating .618034…
and the manner in which the values approach it, until the eye cannot distinguish
them from the line. However, if we wish to be very precise in our study, we
must recognize that it is only when this series is carried out to infinity,
as said before, that this ratio between the consecutive terms becomes .618034…
We discover the series for which we are looking if we will take .618034…
as one of its terms, and subtract it from 1.000, giving us .381966… By
adding any two consecutive terms in order to give us the following one, we shall
find that the series grows as follows:
.382, .618, 1.00, 1.618, 2.618, 4.236, 6,854,
and so on.
This series of numbers is an arithmetical
series for the reason that it increases to the right by a process of addition.
Thus, each term is the sum of the two preceding terms.
*************************************************************
Fig. 22 — The Golden Section and the Fibonacci Series.
*************************************************************
It is also a geometrical progression for
the reason that it is generated by a process of multiplication. The factor
.618 is a constant. Thus, each term is .618 times the term to the right.
This is a series of numbers which extends indefinitely in both directions,
so it does not really start with .382. We may extend it indefinitely to the
left. So it is now presented with a value 1.00 as occupying a central position:
| .090 |
.146 |
.236 |
.382 |
.618 |
1.00 |
1.618 |
2.618 |
4.236 |
6.854 |
11.090 |
| -5 |
-4 |
-3 |
-2 |
-1 |
|
1 |
2 |
3 |
4 |
5 |
The number under each term of this series
indicates its place to the left or the right of 1.00. This is done in order
to bring out a most curious property of this series. To multiply two or more
terms of this series, take the algebraic sum of their subscripts and locate
the product above the new subscript. Two examples will make this clear: Multiply
.236 by .6854. Their subscripts are —3 and 4, the algebraic sum of which is
1. Locate 1.618 over subscript 1.
Multiply .618 by .146. Their subscripts
are — 1 and — 4, the algebraic sum of which is —5. Locate .090 above subscript
—5.
To find the square of any term, multiply
its subscript by 2, and locate the answer. Thus the square of .382 is .146.
The square of 1.618 is 2.618. Since each term is the sum of the two terms preceding
it, the formula
a : b = b : c becomes a : b = b: (a + b)
We are ready to move into a geometrical
consideration of the Golden Section; this should be introduced by stating that
a rectangle constructed such that the height and width are any two consecutive
terms of this series, will be proportioned as .618 : 1.00. This is held to
be the most beautifully proportioned of all rectangles, and the Greeks recognized
this. They used it widely in their architecture, their ornaments, statuary,
vases and paintings. We shall henceforth refer to it as a Golden Rectangle.
In order that we may construct this rectangle
and other figures, we must learn how to divide a line at the point of the Golden
Section. See upper part of Fig. 22.
Upon a given line AB, erect a perpendicular
AC at point A, equal to one half of AB.
Join BC.
With C as center, and with radius CA, describe
an arc cutting CB at K.
With center at B, and with radius BK, describe
an arc cutting AB at point P. P is the point of the Golden Section, and AP
: PB as PB : AB. Expressed in words, the shorter line segment is to the longer
line segment as the longer is to the whole line. This satisfies the equation
a : b = b : ( a + b).
To present the geometrical proof of this
might be confusing to some readers, as a knowledge of several geometrical principles
involving the relationship between tangents and secants to a circle would be
required. This material is readily available in any standard textbook on Plane
Geometry, and it is better to confine ourselves to a consideration of the numerical
relationships which apply to the Golden Section of the line AB.
Let us consider that the perpendicular AC equals 1.00, and
the line AB equals 2.00. BC is the hypotenuse of the right triangle ABC and
is therefore the square root of the sum of the squares of the sides AC and AB,
1² + 2² = 5. Thus, BC equals the square root of 5, or 2.236. BK equals BC
— KC, or 2.236 - 1.00. This means that BK equals 1.26. Marking off this length
on AB at the point P, gives us a ratio of 1.26 : 2. This reduces to .618 :
1.00, or the Golden Section of the line.
This is expressed algebraically as the square root of 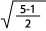 .
AP must equal 2.00 - 1.236, or .764, and the ratio of 7.64 : 2.00 reduces to
.382 : 1.00. Thus we have three terms in the Golden Series: .382, .618, and 1.00.
.
AP must equal 2.00 - 1.236, or .764, and the ratio of 7.64 : 2.00 reduces to
.382 : 1.00. Thus we have three terms in the Golden Series: .382, .618, and 1.00.
Now there is a second point, P', which balances
the point P. It may be found by erecting the perpendicular at B; but for simplicity
of explanation this point P' is shown without the construction which would only
duplicate what has already been done. The point P' not only divides the line
AB at the point of the Golden Section, but it also divides PB in the same manner.
Thus we have four terms in the Golden Series, since PP' is .236.
If we wish to construct a Golden Rectangle,
we have only to construct a square as in Fig. 23. M is the midpoint of the
base of the square; with M as a center, and the length MC as a radius, describe
an arc cutting AB produced, at the point E. Erect a perpendicular at point
E, to meet DC produced, at the point F. Rectangle AEFD is a Golden Rectangle,
and the width (or height) EF is to the length (or base) AE as .618 : 1.00.
The diagonal of the Golden Rectangle, AF,
is interesting. If we were to construct a circle with radius AE we would find
that the diagonal AF is the length of the side of an inscribed regular pentagon.
Also, the height of the rectangle, EF, is the side of an inscribed regular decagon.
The smaller rectangle at the side of the square (standing on its shorter side)
is also a Golden Rectangle, and therefore similar to the rectangle AEFD, and
its diagonal, EC, is perpendicular to the longer diagonal AF.
**********************************************************
Fig. 23 — The “Golden” Rectangle.
**********************************************************
**********************************************************
Fig. 24 — The Rectangle of the Whirling Squares
**********************************************************
Their intersection is the
“eye” of an intersecting series of squares which appear to rotate about (Figure
24 shows this as a “rectangle of the whirling squares”).
Figure 25 shows one of the triangle segments
of a regular Decagon, generated by the moving circle as in Chapter II. Its
sides would be two of the radii of the circle, and its base is one side of the
polygon. We demonstrated at that time that numerically its length is .618 of
the radius, but the geometrical proof that it actually is a regular decagon
was left to this later time. thus we must prove that the angle at the apex
of the triangle is 36º. Having done this, we shall not only find that the proposition
of the moving circle is geometrically correct, but that we have here a triangle
of truly remarkable properties.
Given isosceles triangle ABC such that AC
and BC are equal, and the base AB is .618 of AC. to prove that the angle at
C contains 36º.
With A as center, and with radius AB, describe an arc cutting BC at K. Join
AK.
Triangle ABK is isosceles because AB equals AK. Therefore Ð AKB = ÐABK.
But ÐCAB = ÐABC, as they are the base angles
of the isosceles triangle ABAC.
Therefore ÐCAB = ÐAKB, and the two triangles are
similar.
Therefore ÐKAB = ÐACB.
Since AB : AC = .618 : 1.00, KB : AB = .618:1.00.
Corresponding parts of similar triangles are proportional.
The Golden Series of terms that we have just studied shows us that KB = .382.
CK = CB - KB, or 1.00 - .382. Therefore CK = .618.
**********************************************************
Fig. 25 — A “Golden” Triangle
**********************************************************
But AK, being equal to AB, is also equal to .618; therefore the triangle
ACK is isosceles with the sides AK and CK equal: the base angles ACK and CAK
are also equal.
Therefore 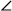 CAK
=
CAK
= 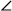 ACK, which also equals
ACK, which also equals 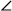 KAB, and
KAB, and 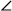 CAB is 2
CAB is 2 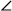 KAB.
KAB.
Therefore each of the base angles of triangle ABC is equal to 2 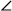 KAB.
KAB.
But 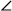 KAB =
KAB = 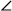 ACB, so that each of the base
angles is equal to 2
ACB, so that each of the base
angles is equal to 2 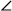 ACB.
ACB.
Therefore the sum of all the angles of triangle ABC = 5 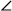 ACB.
ACB.
The sum of the angles of any triangle is 180°. Therefore 180° is 5 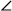 ACB.
ACB.
Therefore 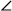 ACB = 36°, and the polygon within the circle
is proven to be a regular decagon.
ACB = 36°, and the polygon within the circle
is proven to be a regular decagon.
The base angles of triangle ABC are each
equal to 72°. Much importance has already been attached to the
number 72.
It is worth noting that in the original
triangle, the base is to the side as .618 : 1.00, and the triangle ACK, the
side is to the base as .618 : 1.00. These triangles were held by the Greeks
to be so important that they were named after the two stars in the sky associated
with the constellation Gemini, the Twins: Castor and Pollux. These triangles
are repeated many times in the five-pointed star diagrams that we have studied.
By repeating the process in the formation
of these triangles from the original triangle ABC, we can subdivide endlessly,
making a series of “whirling triangles,” and we find that they form the basis
of an interesting logarithmic spiral which is similar in shape to the shells
of certain sea-creatures. Numerous instances can be found in nature, wherein
the Golden Section plays its part in natural design.
***********************************************************
Fig. 26 — Constructing a Pentagon Within a Circle
***********************************************************
Fig. 26 shows how to construct an inscribed
regular Pentagon within a circle. Given circle with center O, construct the
diameter AB and CD mutually perpendicular.
***********************************************************
Fig. 27 — Constructing a Pentagon, having given one Side.
***********************************************************
M is the midpoint of OB, and with M as a
center, and with radius MC, describe an arc cutting AO at the point P. With
C as center, and with radius CP, describe an arc cutting the circumference at
P'. CP' is the side of the inscribed pentagon.
Figure 27 shows how to construct a regular Pentagon having one of its sides
given. Given side AB, on A construct a perpendicular AC equal to ½ AB.
Join BC and extend.
With C as center, and radius CA, describe an arc cutting BC extended at point
P.
With B as center, and radius BP, describe an arc; and then with A as center,
and with the same radius, describe another arc.
Point X is the intersection of these arcs.
With A as center, and with radius AB, describe an arc cutting arc PX at P'.
With B as center, and with radius AB, describe an arc cutting arc XY at Q.
Join points A, P;, X, Q and B to complete the pentagon.
***********************************************************
Fig. 28 — Constructing a Pentagram (Five-pointed Star), having given one Side.
***********************************************************
Figure 28 shows how to construct a five-pointed
star, having given one of its lines, AB.
Upon AB locate the two points P and P' of the Golden Section by the method
already explained.
With P as center, and with radius PA, describe an arc upwards.
With P' as center, and with radius P'B, describe an arc upwards. Locate
Point C where the arcs intersect. Join CP and extend. Join CP' and extend.
Set the compass to radius AB. With C as center, describe an arc cutting
CP extended at point D, and CP' extended at point E. Join AE and BD to complete
the star.
![]() CAK
=
CAK
= ![]() ACK, which also equals
ACK, which also equals ![]() KAB, and
KAB, and ![]() CAB is 2
CAB is 2 ![]() KAB.
KAB.![]() KAB.
KAB.![]() KAB =
KAB = ![]() ACB, so that each of the base
angles is equal to 2
ACB, so that each of the base
angles is equal to 2 ![]() ACB.
ACB.![]() ACB.
ACB.![]() ACB.
ACB.![]() ACB = 36°, and the polygon within the circle
is proven to be a regular decagon.
ACB = 36°, and the polygon within the circle
is proven to be a regular decagon.