The Project Gutenberg EBook of Experimental Determination of the Velocity
of Light, by Albert A. Michelson

This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever.  You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.net


Title: Experimental Determination of the Velocity of Light
       Made at the U.S. Naval Academy, Annapolis

Author: Albert A. Michelson

Release Date: March 28, 2004 [EBook #11753]

Language: English

Character set encoding: Unicode UTF-8

*** START OF THIS PROJECT GUTENBERG EBOOK VELOCITY OF LIGHT ***




Page images provided by Case Western Reserve University's Digital
Preservation Department

Introduction.

In Cornu's elaborate memoir upon the determination of the velocity of light, several objections are made to the plan followed by Foucault, which will be considered in the latter part of this work. It may, however, be stated that the most important among these was that the deflection was too small to be measured with the required degree of accuracy. In order to employ this method, therefore, it was absolutely necessary that the deflection should be increased.

In November, 1877, a modification of Foucault's arrangement suggested itself, by which this result could be accomplished. Between this time and March of the following year a number of preliminary experiments were performed in order to familiarize myself with the optical arrangements. The first experiment tried with the revolving mirror produced a deflection considerably greater than that obtained by Foucault. Thus far the only apparatus used was such as could be adapted from the apparatus in the laboratory of the Naval Academy.

At the expense of $10 a revolving mirror was made, which could execute 128 turns per second. The apparatus was installed in May, 1878, at the laboratory. The distance used was 500 feet, and the deflection was about twenty times that obtained by Foucault.[1]

These experiments, made with very crude apparatus and under great difficulties, gave the following table of results for the velocity of light in miles per second:

186730
188820
186330
185330
187900
184500
186770
185000
185800
187940
------
Mean 186500 ± 300 miles per second, or 300140 kilometers per second.

In the following July the sum of $2,000 was placed at my disposal by a private gentleman for carrying out these experiments on a large scale. Before ordering any of the instruments, however, it was necessary to find whether or not it was practicable to use a large distance. With a distance (between the revolving and the fixed mirror) of 500 feet, in the preliminary experiments, the field of light in the eye-piece was somewhat limited, and there was considerable indistinctness in the image, due to atmospheric disturbances.

Accordingly, the same lens (39 feet focus) was employed, being placed, together with the other pieces of apparatus, along the north sea-wall of the Academy grounds, the distance being about 2,000 feet. The image of the slit, at noon, was so confused as not to be recognizable, but toward sunset it became clear and steady, and measurements were made of its position, which agreed within one one-hundredth of a millimeter. It was thus demonstrated that with this distance and a deflection of 100 millimeters this measurement could be made within the ten-thousandth part.

In order to obtain this deflection, it was sufficient to make the mirror revolve 250 times per second and to use a "radius" of about 30 feet. In order to use this large radius (distance from slit to revolving mirror), it was necessary that the mirror should be large and optically true; also, that the lens should be large and of great focal length. Accordingly the mirror was made 1¼ inches in diameter, and a new lens, 8 inches in diameter, with a focal length of 150 feet was procured.

In January, 1879, an observation was taken, using the old lens, the mirror making 128 turns per second. The deflection was about 43 millimeters. The micrometer eye-piece used was substantially the same as Foucault's, except that part of the inclined plate of glass was silvered, thus securing a much greater quantity of light. The deflection having reached 43 millimeters, the inclined plate of glass could be dispensed with, the light going past the observer's head through the slit, and returning 43 millimeters to the left of the slit, where it could be easily observed.

Thus the micrometer eye-piece is much simplified, and many possible sources of error are removed.

The field was quite limited, the diameter being, in fact, but little greater than the width of the slit. This would have proved a most serious objection to the new arrangement. With the new lens, however, this difficulty disappeared, the field being about twenty times the width of the slit. It was expected that, with the new lens, the image would be less distinct; but the difference, if any, was small, and was fully compensated by the greater size of the field.

The first observation with the new lens was made January 30, 1879. The deflection was 70 millimeters. The image was sufficiently bright to be observed without the slightest effort. The first observation with the new micrometer eye-piece was made April 2, the deflection being 115 millimeters.

The first of the final series of observations was made on June 5. All the observations previous to this, thirty sets in all, were rejected. After this time, no set of observations nor any single observation was omitted.

Theory of New Method.

Let S, Fig. 1, be a slit, through which light passes, falling on R, a mirror free to rotate about an axis at right angles to the plane of the paper; L, a lens of great focal length, upon which the light falls which is reflected from R. Let M be a plane mirror whose surface is perpendicular to the line R, M, passing through the centers of R, L, and M, respectively. If L be so placed that an image of S is formed on the surface of M, then, this image acting as the object, its image will be formed at S, and will coincide, point for point, with S.

If, now, R be turned about the axis, so long as the light falls upon the lens, an image of the slit will still be formed on the surface of the mirror, though on a different part, and as long as the returning light falls on the lens an image of this image will be formed at S, notwithstanding the change of position of the first image at M. This result, namely, the production of a stationary image of an image in motion, is absolutely necessary in this method of experiment. It was first accomplished by Foucault, and in a manner differing apparently but little from the foregoing.

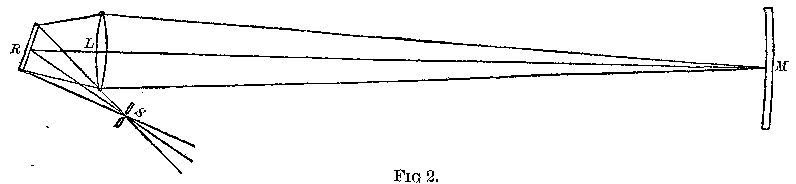
In his experiments L, Fig. 2, served simply to form the image of S at M, and M, the returning mirror, was spherical, the center coinciding with the axis of R. The lens L was placed as near as possible to R. The light forming the return image lasts, in this case, while the first image is sweeping over the face of the mirror, M. Hence, the greater the distance RM, the larger must be the mirror in order that the same amount of light may be preserved, and its dimensions would soon become inordinate. The difficulty was partly met by Foucault, by using five concave reflectors instead of one, but even then the greatest distance he found it practicable to use was only 20 meters.

Returning to Fig. 1, suppose that R is in the principal focus of the lens L; then, if the plane mirror M have the same diameter as the lens, the first, or moving image, will remain upon M as long as the axis of the pencil of light remains on the lens, and this will be the case no matter what the distance may be.

When the rotation of the mirror R becomes sufficiently rapid, then the flashes of light which produce the second or stationary image become blended, so that the image appears to be continuous. But now it no longer coincides with the slit, but is deflected in the direction of rotation, and through twice the angular distance described by the mirror, during the time required for light to travel twice the distance between the mirrors. This displacement is measured by the tangent of the arc it subtends. To make this as large as possible, the distance between the mirrors, the radius, and the speed of rotation should be made as great as possible.

The second condition conflicts with the first, for the radius is the difference between the focal length for parallel rays, and that for rays at the distance of the fixed mirror. The greater the distance, therefore, the smaller will be the radius.

There are two ways of solving the difficulty: first, by using a lens of great focal length; and secondly, by placing the revolving mirror within the principal focus of the lens. Both means were employed. The focal length of the lens was 150 feet, and the mirror was placed about 15 feet within the principal focus. A limit is soon reached, however, for the quantity of light received diminishes very rapidly as the revolving mirror approaches the lens.

Arrangement and Description of Apparatus.

Site and Plan.

The site selected for the experiments was a clear, almost level, stretch along the north sea-wall of the Naval Academy. A frame building was erected at the western end of the line, a plan of which is represented in Fig. 3.

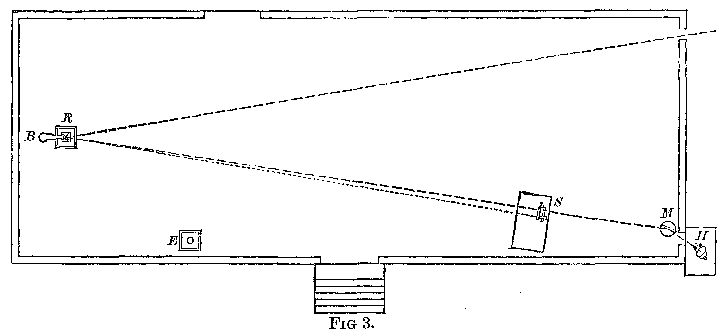
The building was 45 feet long and 14 feet wide, and raised so that the line along which the light traveled was about 11 feet above the ground. A heliostat at H reflected the sun's rays through the slit at S to the revolving mirror R, thence through a hole in the shutter, through the lens, and to the distant mirror.

The Heliostat.

The heliostat was one kindly furnished by Dr. Woodward, of the Army Medical Museum, and was a modification of Foucault's form, designed by Keith. It was found to be accurate and easy to adjust. The light was reflected from the heliostat to a plane mirror, M, Fig. 3, so that the former need not be disturbed after being once adjusted.

The Revolving Mirror.

The revolving mirror was made by Fauth & Co., of Washington. It consists of a cast-iron frame resting on three leveling screws, one of which was connected by cords to the table at S, Fig. 3, so that the mirror could be inclined forward or backward while making the observations.

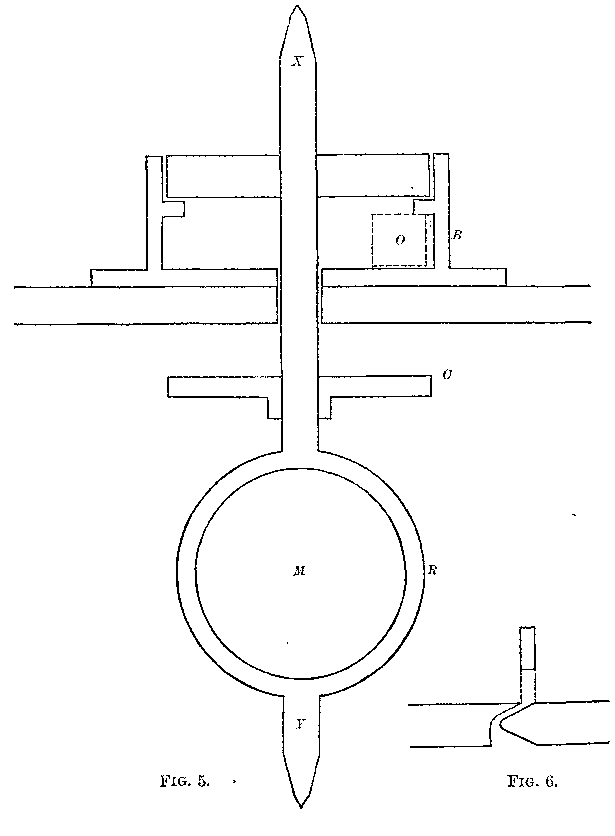
Two binding screws, S, S, Fig. 4, terminating in hardened steel conical sockets, hold the revolving part. This consists of a steel axle, X, Y, Figs. 4 and 5, the pivots being conical and hardened. The axle expands into a ring at R, which holds the mirror M. The latter was a disc of plane glass, made by Alvan Clark & Sons, about 1¼ inch in diameter and 0.2 inch thick. It was silvered on one side only, the reflection taking place from the outer or front surface. A species of turbine wheel, T, is held on the axle by friction. This wheel has six openings for the escape of air; a section of one of them is represented in Fig 6.

Adjustment of the Revolving Mirror.

The air entering on one side at O, Fig. 5, acquires a rotary motion in the box B, B, carrying the wheel with it, and this motion is assisted by the reaction of the air in escaping. The disc C serves the purpose of bringing the center of gravity in the axis of rotation. This was done, following Foucault's plan, by allowing the pivots to rest on two inclined planes of glass, allowing the arrangement to come to rest, and filing away the lowest part of the disc; trying again, and so on, till it would rest in indifferent equilibrium. The part corresponding to C, in Foucault's apparatus, was furnished with three vertical screws, by moving which the axis of figure was brought into coincidence with the axis of rotation. This adjustment was very troublesome. Fortunately, in this apparatus it was found to be unnecessary.

When the adjustment is perfect the apparatus revolves without giving any sound, and when this is accomplished, the motion is regular and the speed great. A slight deviation causes a sound due to the rattling of the pivots in the sockets, the speed is very much diminished, and the pivots begin to wear. In Foucault's apparatus oil was furnished to the pivots, through small holes running through the screws, by pressure of a column of mercury. In this apparatus it was found sufficient to touch the pivots occasionally with a drop of oil.

Fig. 7 is a view of the turbine, box, and supply-tube, from above. The quantity of air entering could be regulated by a valve to which was attached a cord leading to the observer's table.

The instrument was mounted on a brick pier.

The Micrometer.

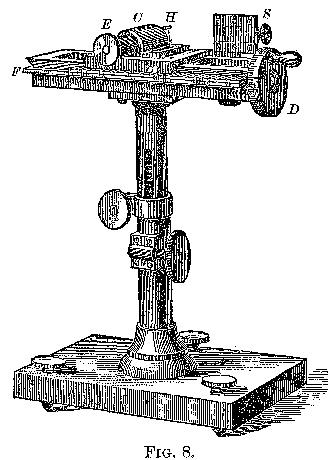
The apparatus for measuring the deflection was made by Grunow, of New York.

This instrument is shown in perspective in Fig. 8, and in plan by Fig. 9. The adjustable slit S is clamped to the frame F. A long millimeter-screw, not shown in Fig. 8, terminating in the divided head D, moves the carriage C, which supports the eye-piece E. The frame is furnished with a brass scale at F for counting revolutions, the head counting hundredths. The eye-piece consists of a single achromatic lens, whose focal length is about two inches. At its focus, in H, and in nearly the same plane as the face of the slit, is a single vertical silk fiber. The apparatus is furnished with a standard with rack and pinion, and the base furnished with leveling screws.

Manner of Using the Micrometer.

In measuring the deflection, the eye-piece is moved till the cross-hair bisects the slit, and the reading of the scale and divided head gives the position. This measurement need not be repeated unless the position or width of the slit is changed. Then the eye-piece is moved till the cross-hair bisects the deflected image of the slit; the reading of scale and head are again taken, and the difference in readings gives the deflection. The screw was found to have no lost motion, so that readings could be taken with the screw turned in either direction.

Measurement of Speed of Rotation.

To measure the speed of rotation, a tuning-fork, bearing on one prong a steel mirror, was used. This was kept in vibration by a current of electricity from five "gravity" cells. The fork was so placed that the light from the revolving mirror was reflected to a piece of plane glass, in front of the lens of the eye-piece of the micrometer, inclined at an angle of 45°, and thence to the eye. When fork and revolving mirror are both at rest, an image of the revolving mirror is seen. When the fork vibrates, this image is drawn out into a band of light.

When the mirror commences to revolve, this band breaks up into a number of moving images of the mirror; and when, finally, the mirror makes as many turns as the fork makes vibrations, these images are reduced to one, which is stationary. This is also the case when the number of turns is a submultiple. When it is a multiple or simple ratio, the only difference is that there are more images. Hence, to make the mirror execute a certain number of turns, it is simply necessary to pull the cord attached to the valve to the right or left till the images of the revolving mirror come to rest.

The electric fork made about 128 vibrations per second. No dependence was placed upon this rate, however, but at each set of observations it is compared with a standard Ut₃ fork, the temperature being noted at the same time. In making the comparison the sound-beats produced by the forks were counted for 60 seconds. It is interesting to note that the electric fork, as long as it remained untouched and at the same temperature, did not change its rate more than one or two hundredths vibrations per second.

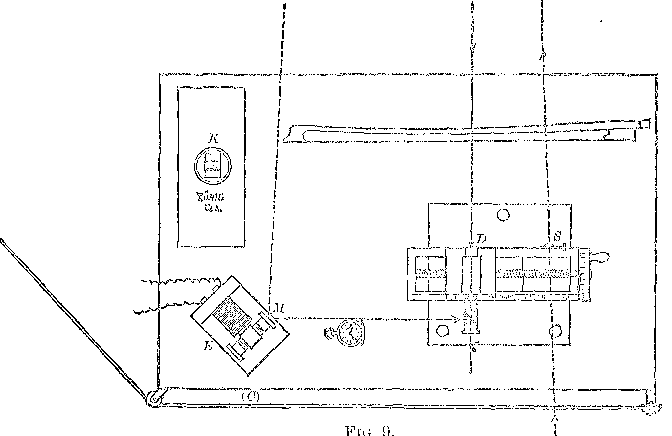
The Observer's Table.

Fig. 9 Represents The Table At Which The Observer Sits. The Light From The Heliostat Passes Through The Slit At S, Goes To The Revolving Mirror, &c., And, On Its Return, Forms An Image Of The Slit At D, Which Is Observed Through The Eye-piece. E Represents The Electric Fork (the Prongs Being Vertical) Bearing The Steel Mirror M. K Is The Standard Fork On Its Resonator. C Is The Cord Attached To The Valve Supplying Air To The Turbine.

The Lens.

The lens was made by Alvan Clark & Sons. It was 8 inches in diameter; focal length, 150 feet; not achromatic. It was mounted in a wooden frame, which was placed on a support moving on a slide, about 16 feet long, placed about 80 feet from the building. As the diameter of the lens was so small in comparison with its focal length, its want of achromatism was inappreciable. For the same reason, the effect of "parallax" (due to want of coincidence in the plane of the image with that of the silk fiber in the eye-piece) was too small to be noticed.

The Fixed Mirror.

The fixed mirror was one of those used in taking photographs of the transit of Venus. It was about 7 inches in diameter, mounted in a brass frame capable of adjustment in a vertical and a horizontal plane by screw motion. Being wedge-shaped, it had to be silvered on the front surface. To facilitate adjustment, a small telescope furnished with cross-hairs was attached to the mirror by a universal joint. The heavy frame was mounted on a brick pier, and the whole surrounded by a wooden case to protect it from the sun.

Adjustment of the Fixed Mirror.

The adjustment was effected as follows: A theodolite was placed at about 100 feet in front of the mirror, and the latter was moved about by the screws till the observer at the theodolite saw the image of his telescope reflected in the center of the mirror. Then the telescope attached to the mirror was pointed (without moving the mirror itself) at a mark on a piece of card-board attached to the theodolite. Thus the line of collimation of the telescope was placed at right angles to the surface of the mirror. The theodolite was then moved to 1,000 feet, and, if found necessary, the adjustment was repeated. Then the mirror was moved by the screws till its telescope pointed at the hole in the shutter of the building. The adjustment was completed by moving the mirror, by signals, till the observer, looking through the hole in the shutter, through a good spy-glass, saw the image of the spy-glass reflected centrally in the mirror.

The whole operation was completed in a little over an hour.

Notwithstanding the wooden case about the pier, the mirror would change its position between morning and evening; so that the last adjustment had to be repeated before every series of experiments.

Apparatus for Supplying and Regulating the Blast of Air.

Fig. 10 represents a plan of the lower floor of the building. E is a three-horse power Lovegrove engine and boiler, resting on a stone foundation; B, a small Roots' blower; G, an automatic regulator. From this the air goes to a delivery-pipe, up through the floor, and to the turbine. The engine made about 4 turns per second and the blower about 15. At this speed the pressure of the air was about half a pound per square inch.

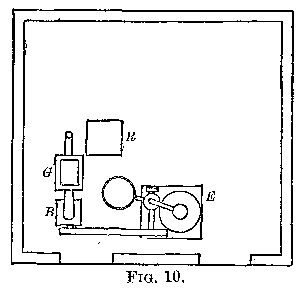
The regulator, Fig. 11, consists of a strong bellows supporting a weight of 370 pounds, partly counterpoised by 80 pounds in order to prevent the bellows from sagging. When the pressure of air from the blower exceeds the weight, the bellows commences to rise, and, in so doing, closes the valve V.

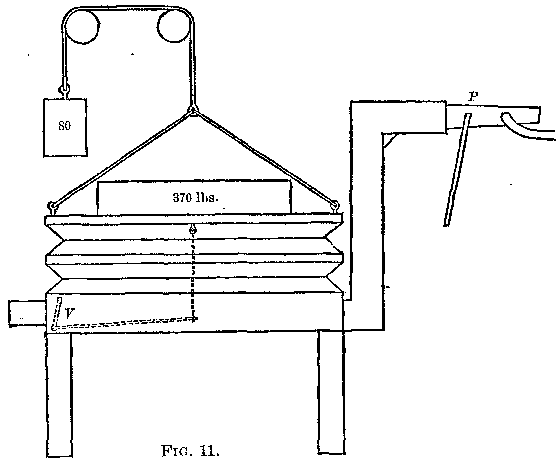
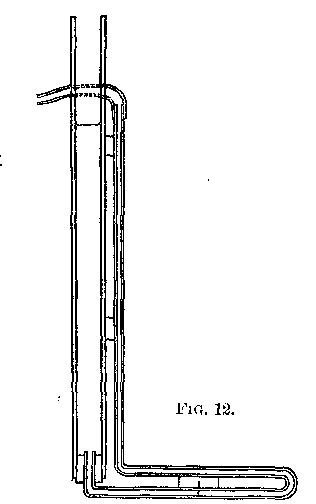
This arrangement was found in practice to be insufficient, and the following addition was made: A valve was placed at P, and the pipe was tapped a little farther on, and a rubber tube led to a water-gauge, Fig 12. The column of water in the smaller tube is depressed, and, when it reaches the horizontal part of the tube, the slightest variation of pressure sends the column from one end to the other. This is checked by an assistant at the valve; so that the column of water is kept at about the same place, and the pressure thus rendered very nearly constant. The result was satisfactory, though not in the degree anticipated. It was possible to keep the mirror at a constant speed for three or four seconds at a time, and this was sufficient for an observation. Still it would have been more convenient to keep it so for a longer time.

I am inclined to think that the variations were due to changes in the friction of the pivots rather than to changes of pressure of the blast of air.

It may be mentioned that the test of uniformity was very delicate, as a change of speed of one or two hundredths of a turn per second could easily be detected.

Method Followed in Experiment.

It was found that the only time during the day when the atmosphere was sufficiently quiet to get a distinct image was during the hour after sunrise, or during the hour before sunset. At other times the image was "boiling" so as not to be recognizable. In one experiment the electric light was used at night, but the image was no more distinct than at sunset, and the light was not steady.

The method followed in experiment was as follows: The fire was started half an hour before, and by the time everything was ready the gauge would show 40 or 50 pounds of steam. The mirror was adjusted by signals, as before described. The heliostat was placed and adjusted. The revolving mirror was inclined to the right or left, so that the direct reflection of light from the slit, which otherwise would flash into the eye-piece at every revolution, fell either above or below the eye-piece.[2]

The revolving mirror was then adjusted by being moved about, and inclined forward and backward, till the light was seen reflected back from the distant mirror. This light was easily seen through the coat of silver on the mirror.

The distance between the front face of the revolving mirror and the cross-hair of the eye-piece was then measured by stretching from the one to the other a steel tape, making the drop of the catenary about an inch, as then the error caused by the stretch of the tape and that due to the curve just counterbalance each other.

The position of the slit, if not determined before, was then found as before described. The electric fork was started, the temperature noted, and the sound-beats between it and the standard fork counted for 60 seconds. This was repeated two or three times before every set of observations.

The eye-piece of the micrometer was then set approximately[3] and the revolving mirror started. If the image did not appear, the mirror was inclined forward or backward till it came in sight.

The cord connected with the valve was pulled right or left till the images of the revolving mirror, represented by the two bright round spots to the left of the cross-hair, came to rest. Then the screw was turned till the cross-hair bisected the deflected image of the slit. This was repeated till ten observations were taken, when the mirror was stopped, temperature noted, and beats counted. This was called a set of observations. Usually five such sets were taken morning and evening.

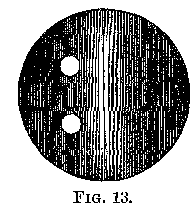
Fig. 13 represents the appearance of the image of the slit as seen in the eye-piece magnified about five times.

Determination of The Constants.

Comparison of the Steel Tape with the Standard Yard.

The steel tape used was one of Chesterman's, 100 feet long. It was compared with Wurdeman's copy of the standard yard, as follows:

Temperature was 55° Fahr.

The standard yard was brought under the microscopes of the comparator; the cross-hair of the unmarked microscope was made to bisect the division marked o, and the cross-hair of the microscope, marked I, was made to bisect the division marked 36. The reading of microscope I was taken, and the other microscope was not touched during the experiment. The standard was then removed and the steel tape brought under the microscopes and moved along till the division marked 0.1 (feet) was bisected by the cross-hair of the unmarked microscope. The screw of microscope I was then turned till its cross-hair bisected the division marked 3.1 (feet), and the reading of the screw taken. The difference between the original reading and that of each measurement was noted, care being taken to regard the direction in which the screw was turned, and this gave the difference in length between the standard and each succesive portion of the steel tape in terms of turns of the micrometer-screw.

To find the value of one turn, the cross-hair was moved over a millimeter scale, and the following were the values obtained:

Turns of screw of microscope I in 1^mm—

7.68	7.73	7.60	7.67
7.68	7.62	7.65	7.57
7.72	7.70	7.64	7.69
7.65	7.59	7.63	7.64
7.55	7.65	7.61	7.63
Mean =7.65
Hence one turn = 0.1307mm.
or = 0.0051 inch.
The length of the steel tape from 0.1 to 99.1 was found to be greater than 33 yards, by 7.4 turns =.96mm			+.003 feet.
Correction for temperature			+.003 feet.
Length			100.000 feet.
			--------------
Corrected length			100.006 feet.

Determination of the Value of Micrometer.

Two pairs of lines were scratched on one slide of the slit, about 38^mm apart, i.e., from the center of first pair to center of second pair. This distance was measured at intervals of 1^mm through the whole length of the screw, by bisecting the interval between each two pairs by the vertical silk fiber at the end of the eye-piece. With these values a curve was constructed which gave the following values for this distance, which we shall call D′:

Turns of screw.

At	0	of scale D′	=38.155
	10	of scale D′	38.155
	20	of scale D′	38.150
	30	of scale D′	38 150
	40	of scale D′	38.145
	50	of scale D′	38.140
	60	of scale D′	38.140
	70	of scale D′	38.130
	80	of scale D′	38.130
	90	of scale D′	38.125
	100	of scale D′	38.120
	110	of scale D′	38.110
	120	of scale D′	38.105
	130	of scale D′	38.100
	140	of scale D′	38.100

Changing the form of this table, we find that,—

For the first
10	turns the average value of D′ is	38.155
20	turns	38.153
30	turns	38.152
40	turns	38.151
50	turns	38.149
60	turns	38.148
70	turns	38.146
80	turns	38.144
90	turns	38.142
100	turns	38.140
110	turns	38.138
120	turns	38.135
130	turns	38.132
140	turns	38.130

On comparing the scale with the standard meter, the temperature being 16°.5 C., 140 divisions were found to = 139.462^mm. This multiplied by (1 + .0000188 × 16.5) = 139.505^mm.

One hundred and forty divisions were found to be equal to 140.022 turns of the screw, whence 140 turns of the screw = 139.483^mm, or 1 turn of the screw = 0.996305^mm.

This is the average value of one turn in 140.

But the average value of D, for 140 turns is, from the preceding table, 38.130.

Therefore, the true value of D, is 38.130 × .996305^mm, and the average value of one turn for 10, 20, 30, etc., turns, is found by dividing 38.130 × .996305 by the values of D;, given in the table.

This gives the value of a turn—

			mm.
For the first	10	turns	0.99570
	20	turns	0.99570
	30	turns	0.99573
	40	turns	0.99577
	50	turns	0.99580
	60	turns	0.99583
	70	turns	0.99589
	80	turns	0.99596
	90	turns	0.99601
	100	turns	0.99606
	110	turns	0.99612
	120	turns	0.99618
	130	turns	0.99625
	140	turns	0.99630

Note.—The micrometer has been sent to Professor Mayer, of Hoboken, to test the screw again, and to find its value. The steel tape has been sent to Professor Rogers, of Cambridge, to find its length again. (See page 145.)

Measurement of the Distance between the Mirrors.

Square lead weights were placed along the line, and measurements taken from the forward side of one to forward side of the next. The tape rested on the ground (which was very nearly level), and was stretched by a constant force of 10 pounds.

The correction for length of the tape (100.006) was +0.12 of a foot.

To correct for the stretch of the tape, the latter was stretched with a force of 15 pounds, and the stretch at intervals of 20 feet measured by a millimeter scale.

mm.

At	100	feet the stretch was	8.0
	80	feet the stretch was	5.0
	60	feet the stretch was	5.0
	40	feet the stretch was	3.5
	20	feet the stretch was	1.5
	---		---
	300		23.00

Weighted mean	=	7.7 mm.
For 10 pounds, stretch	=	5.1 mm.
	=	0.0167 feet.
Correction for whole distance	=	+0.33 feet.

The following are the values obtained from five separate measurements of the distance between the caps of the piers supporting the revolving mirror and the distant reflector; allowance made in each case for effect of temperature:

	1985.13	feet.
	1985.17	feet.
	1984.93	feet.
	1985.09	feet.
	1985.09	feet.
	-------
Mean =	1985.082	feet.
	+.70.	Cap of pier to revolving mirror.
	+.33.	Correction for stretch of tape.
	+.12.	Correction for length of tape.
	--------
	1986.23.	True distance between mirrors.

Rate of Standard Ut₃ Fork.

The rate of the standard Ut₃ fork was found at the Naval Academy, but as so much depended on its accuracy, another series of determinations of its rate was made, together with Professor Mayer, at the Hoboken Institute of Technology.

Set of determinations made at Naval Academy.

The fork was armed with a tip of copper foil, which was lost during the experiments and replaced by one of platinum having the same weight, 4.6 mgr. The fork, on its resonator, was placed horizontally, the platinum tip just touching the lampblacked cylinder of a Schultze chronoscope. The time was given either by a sidereal break-circuit chronometer or by the break-circuit pendulum of a mean-time clock. In the former case the break-circuit worked a relay which interrupted the current from three Grove cells. The spark from the secondary coil of an inductorium was delivered from a wire near the tip of the fork. Frequently two sparks near together were given, in which case the first alone was used. The rate of the chronometer, the record of which was kept at the Observatory, was very regular, and was found by observations of transits of stars during the week to be +1.3 seconds per day, which is the same as the recorded rate.

Specimen of a Determination of Rate of Ut₃ Fork.

Temp.=27° C. Column 1 gives the number of the spark or the number of the second. Column 2 gives the number of sinuosities or vibrations at the corresponding second. Column 3 gives the difference between 1 and 11, 2 and 12, 3 and 13, etc.

July 4, 1879.

1.	0.1	2552.0
2.	255.3	2551.7
3.	510.5	2551.9
4.	765.6	2551.9
5.	1020.7	2552.1
6.	1275.7	2552.0
7.	1530.7	2551.8
8.	1786.5	2551.4
9.	2041.6	2551.7
10.	2297.0	2551.5
		-------
11.	2552.1	255.180	= mean ÷ 10.
12.	2807.0	+ .699	= reduction for mean time.
13.	3062.4	+ .003	= correction for rate.
14.	3317.5	+ .187	= correction for temperature.
		-------
15.	3572.8	256.069	= number of vibrations per second at 65° Fahr.
16.	3827.7
17.	4082.5
18.	4335.9
19.	4593.3
20.	4848.5

The correction for temperature was found by Professor Mayer by counting the sound-beats between the standard and another Ut₃ fork, at different temperatures. His result is +.012 vibrations per second for a diminution of 1° Fahr. Using the same method, I arrived at the result +.0125. Adopted +.012.

Résumé of determinations made at Naval Academy.

In the following table the first column gives the date, the second gives the total number of seconds, the third gives the result uncorrected for temperature, the fourth gives the temperature (centigrade), the fifth gives the final result, and the sixth the difference between the greatest and least values obtained in the several determinations for intervals of ten seconds:

July	4	20		255.882	27.0	256.069	0.07
	5	19		255.915	26.4	256.089	0.05
	5	18		255.911	26.0	256.077	0.02
	6	21		255.874	24.7	256.012	0.13
	6	9		255.948	24.8	256.087	0.24
	7	22		255.938	24.6	256.074	0.05
	7	21		255.911	25.3	256.061	0.04
	8	20		255.921	26.6	256.100	0.02
	8	20		255.905	26.6	256.084	0.06
	8	20		255.887	26.6	256.066	0.03
						-------
					Mean =	256.072

In one of the preceding experiments, I compared the two Vt₃ forks while the standard was tracing its record on the cylinder, and also when it was in position as for use in the observations. The difference, if any, was less than .01 vibration per second.

Second determination.

(Joint work with Professor A.M. Mayer, Stevens Institute, Hoboken.)

The fork was wedged into a wooden support, and the platinum tip allowed to rest on lampblacked paper, wound about a metal cylinder, which was rotated by hand Time was given by a break-circuit clock, the rate of which was ascertained, by comparisons with Western Union time-ball, to be 9.87 seconds. The spark from secondary coil of the inductorium passed from the platinum tip, piercing the paper. The size of the spark was regulated by resistances in primary circuit.

The following is a specimen determination:

Column 1 gives the number of the spark or the number of seconds. Column 2 gives the corresponding number of sinuosities or vibrations. Column 3 gives the difference between the 1st and 7th ÷ 6, 2nd and 8th ÷ 6, etc.

1	0.3	255.83
2	256.1	255.90
3	511.7	255.90
4	767.9	255.93
5	1023.5	255.92
6	1289.2	256.01
7	1535.3	255.95
		-------
8	1791.5	255.920	= mean.
9	2047.1	- .028	= correction for rate.
		-------
10	2303.5	255.892
11	2559.0	+ .180	= correction for temperature.
		-------
12	2825.3	256.072	= number of vibrations per second at 65° Fahr.
13	3071.0

In the following résumé, column 1 gives the number of the experiments. Column 2 gives the total number of seconds. Column 3 gives the result not corrected for temperature. Column 4 gives the temperature Fahrenheit. Column 5 gives the final result. Column 6 gives the difference between the greatest and least values:

1	13	255.892	80	256.072	0.18
2	11	255.934	81	256.126	0.17
3	13	255.899	81	256.091	0.12
4	13	255.988	75	256.108	0.13
5	11	255.948	75	256.068	0.05
6	12	255.970	75	256.090	0.05
7	12	255.992	75	256.112	0.20
8	11	255.992	76	256.124	0.03
9	11	255.888	81	256.080	0.13
10	13	255.878	81	256.070	0.13
				-------
			Mean =	256.094

Effect of Support and of Scraping.

The standard Vt₃ fork held in its wooden support was compared with another fork on a resonator loaded with wax and making with standard about five beats per second. The standard was free from the cylinder. The beats were counted by coincidences with the ⅕ second beats of a watch.

Specimen.

Coincidences were marked—

At 32	seconds.
37	seconds.
43.5	seconds.
49	seconds.
54.5	seconds.
61.5	seconds.
61.5 - 32	= 29.5.
29.5 ÷ 5	= 5.9 =	time of one interval.

Résumé.

1	5.9
2	6.2
3	6.2
4	6.2
	----
Mean =	6.13	= time of one interval between coincidences.

In this time the watch makes 6.13×5 = 30.65 beats, and the forks make 30.65 + 1 = 31.65 beats.

Hence the number of beats per second is 31.65 ÷ 6.13 = 5.163.

Specimen.

Circumstances the same as in last case, except that standard Vt₃ fork was allowed to trace its record on the lampblacked paper, as in finding its rate of vibration.

Coincidences were marked at—

59	seconds.
04	seconds.
10.5	seconds.
17	seconds.
77 - 59 = 18.
18 ÷ 3 = 6.0 = time of one interval.

Résumé.

No.	1 6.0	seconds.	6.31 × 5 = 31.55
	2 6.0	seconds.	+ 1.00
	3 6.7	seconds.	----
	4 6.3	seconds.
	5 6.5	seconds.	32.55
	6 6.7	seconds.	32.55 ÷ 6.31 = 5.159
	7 6.0	seconds.	With fork free 5.163
	----		-----
Mean =	6.31	seconds	Effect of scrape = - .044

Specimen.

Circumstances as in first case, except that both forks were on their resonators.

Coincidences were observed at—

21	seconds.
28	seconds.
36	seconds.
44	seconds.
51	seconds.
60	seconds.
60 - 21 = 39
39 ÷ 5 = 7.8 =	time of one interval.

Résumé.

No.	1	7.8	seconds.	7.42 × 5 =	37.10
	2	7.1	seconds.	+	1.00
	3	7.6	seconds.		-----
	4	7.4	seconds.		38.10
	5	7.2	seconds.	38.10 ÷ 7.42 =	5.133
		----		(Above)	5.159
					-----
	Mean =	7.42	seconds. Effect of support and scrape =		- .026
Mean of second determination was					256.094
Applying correction (scrape, etc.)					- .026
					-------
Corrected mean					256.068
Result of first determination					256.072
					-------
Final value					256.070

Note—The result of first determination excludes all work except the series commencing July 4. If previous work is included, and also the result first obtained by Professor Mayer, the result would be 256.089.

	256.180
	256.036
	256.072
	256.068
	-------
Mean =	256.089

The previous work was omitted on account of various inaccuracies and want of practice, which made the separate results differ widely from each other.

The Formulæ.

The formulæ employed are—

	d′
(1) tan φ =	-----
	r
	2592000″ × D × n
(2) V =	-----------------
	φ″
φ =	angle of deflection.
d′ =	corrected displacement (linear).
r =	radius of measurement.
D =	twice the distance between the mirrors.
n =	number of revolutions per second.
α =	inclination of plane of rotation
d =	deflection as read from micrometer.
B =	number of beats per second between electric Vt₂ fork and standard Vt3
Cor =	correction for temperature of standard Vt3.
V =	velocity of light.
T =	value of one turn of screw. (Table, page 126.)

Substituting for d, its value or d×T×sec α (log sec α = .00008), and for D its value 3972.46, and reducing to kilometers, the formulæ become—

		dT
(3) tan φ =	c′	----;	log c′ = .51607
		r
	n
(4) V = c ---;	log c = .49670
	φ
D and r are expressed in feet and d′ in millimeters.
Vt3 fork makes 256.070 vibrations per second at 65° Fahr.
D =	3972.46 feet.
tan α =	tangent of angle of inclination of plane of rotation = 0.02 in all but the last twelve observations, in which it was 0.015.
log c′ =	.51607 (.51603 in last twelve observations.).
log c =	.49670.

The electric fork makes ½(256.070 + B + cor.) vibrations per second, and n is a multiple, submultiple, or simple ratio of this.

Observations.

Specimen Observation.

June 17. sunset. Image good; best in column (4).

The columns are sets of readings of the micrometer for the deflected image of slit.

	112.81	112.80	112.83	112.74	112.79
	81	81	81	76	78
	79	78	78	74	74
	80	75	74	76	74
	79	77	74	76	77
	82	79	72	78	81
	82	73	76	78	77
	76	78	81	79	75
	83	79	74	83	82
	73	73	76	78	82
	-------	-------	-------	-------	-------
Mean =	112.801	112.773	112.769	112.772	112.779
Zero =	0.260	0.260	0.260	0.260	0.260
	-------	-------	-------	-------	-------
d =	112.451	112.513	112.509	112.512	112.519
Temp =	77°	77°	77°	77°	77°
B =	+ 1.500
Corr =	- .144
	-------
	+ 1.365
	256.070
	-------
n =	257.426	257.43	257.43	257.43	257.43
r =	28.157	28.157	28.157	28.157	28.157

The above specimen was selected because in it the readings were all taken by another and noted down without divulging them till the whole five sets were completed.

The following is the calculation for V:

2d, 3d,
	1st set.	and 4th sets.	5th set.
log	c′ =	51607	51607	51607
"	T =	99832	99832	99832
"	d =	05131	05119	05123
		-------	-------	-------
		56570	56558	56562
"	r =	44958	44958	44958
		-------	-------	-------
"	tan φ =	11612	11600	11604
	φ =	2694″.7	2694″.1	2694″.3
"	c =	49670	49670	49670
"	n =	41066	41066	41066
		-------	-------	-------
		90736	90736	90736
"	φ =	43052	43042	43046
		-------	-------	-------
"	V =	47684	47694	47690
	V =	299800	299880	299850

In the following table, the numbers in the column headed "Distinctness of Image" are thus translated: 3, good; 2, fair; 1, poor. These numbers do not, however, show the relative weights of the observations.

The numbers contained in the columns headed "Position of Deflected Image," "Position of Slit," and displacement of image in divisions were obtained as described in the paragraph headed "Micrometer," page 120.

The column headed "B" contains the number of "beats" per second between the electric Vt₂ fork and the standard Vt₃ as explained in the paragraph headed "Measurement of the Speed of Rotation." The column headed "Cor." contains the correction of the rate of the standard fork for the difference in temperature of experiment and 65° Fahr., for which temperature the rate was found. The numbers in the column headed "Number of revolutions per second" were found by applying the corrections in the two preceding columns to the rate of the standard, as explained in the same paragraph.

The "radius of measurement" is the distance between the front face of the revolving mirror and the cross-hair of the micrometer.

The numbers in the column headed "Value of one turn of the screw" were taken from the table, page 127.

Date.	Distinctness of image.	Temperature, Fahr.	Position of deflected image.	Position of slit.	Displacement of image in divisions.	Difference between greatest and least values.	B.	Cor.	Number of revolutions per second.	Radius of measurement, in feet.	Value of one turn of the screw.	Velocity of light in air, in kilometers.	Remarks.
June  5	3	76	114.85	0.300	114.55	0.17	1.423	-0.132	257.36	28.672	0.99614	299850	Electric light.
June  7	2	72	114.64	0.074	114.56	0.10	1.533	-0.084	257.52	28.655	0.99614	299740	P.M. Frame inclined at various angles
June  7	2	72	114.58	0.074	114.50	0.08	1.533	-0.084	257.52	28.647	0.99614	299900	P.M. Frame inclined at various angles
June  7	2	72	85.91	0.074	85.84	0.12	1.533	-0.084	193.14	28.647	0.99598	300070	P.M. Frame inclined at various angles
June  7	2	72	85.97	0.074	85.89	O.07	1.533	-0.084	193.14	28.650	0.99598	299930	P.M. Frame inclined at various angles
June  7	2	72	114.61	0.074	114-53	0.07	1.533	-0.084	257.42	28.650	0.99614	299850	P.M. Frame inclined at various angles
June  9	3	83	114.54	0.074	114.47	0.07	1.533	-0.216	257.39	28.658	0.99614	299950	P.M. Frame inclined at various angles
June  9	3	83	114.54	0.074	114.46	0.10	1.533	-0.216	257.39	28.658	0.99614	299980	P.M. Frame inclined at various angles
June  9	3	83	114.57	0.074	114.47	0.08	1.533	-0.216	257.39	28.662	0.99614	299980	P.M. Frame inclined at various angles
June  9	3	83	114.57	0.074	114.50	0.06	1.533	-0.216	257.39	28.660	0.99614	299880	P.M. Frame inclined at various angles
June  9	2	83	114.61	0.074	114.53	0.13	1.533	-0.216	257.39	28.678	0.99614	300000	P.M. Frame inclined at various angles
June 10	2	90	114.60	0.074	114.52	0.11	1.517	-0.300	257.29	28.685	0.99614	299980	P.M.
June 10	2	90	114.62	0.074	114.54	0.08	1.517	-0.300	257.29	28.685	0.99614	299930	P.M.
June 12	2	71	114.81	0.074	114.74	0.09	1.450	-0.072	257.45	28.690	0.99614	299650	A.M.
June 12	2	71	114.78	0.074	114.70	0.05	1.450	-0.072	257.45	28.690	0.99614	299760	A.M.
June 12	1	71	114.76	0.074	114.68	0.09	1.450	-0.072	257.45	28.690	0.99614	299810	A.M.
June 13	3	72	112.64	0.074	112.56	0.09	1.500	-0.084	257.49	28.172	0.99614	300000	A.M.
June 13	3	72	112.63	0.074	112.56	0.10	1.500	-0.084	257.49	28.172	0.99614	300000	A.M.
June 13	2	72	112.65	0.074	112.57	0.08	1.500	-0.084	257.49	28.172	0.99614	299960	A.M.
June 13	3	79	112.82	0.260	112.56	0.06	1.517	-0.168	257.42	28.178	0.99614	299960	P.M.
June 13	3	79	112.82	0.260	112.56	0.13	1.517	-0.168	257.42	28.178	0.99614	299960	P.M.
June 13	3	79	112.83	0.260	112.57	0.07	1.517	-0.168	257.42	28.178	0.99614	299940	P.M.
June 13	3	79	112.82	0.260	112.56	0.06	1.517	-0.168	257.42	28.178	0.99614	299960	P.M.
June 13	3	79	112.83	0.260	112.57	0.11	1.517	-0.168	257.42	28.178	0.99614	299940	P.M.
June 13	3	79	113.41	0.260	113.15	11	1.517	-0.168	258.70	28.152	0.99614	299880	P.M. Set micrometer and counted oscillations.
June 13	3	79	112.14	0.260	111.88	6	1.517	-0.168	255.69	28.152	0.99614	299800	Oscillations of image of revolving mirror.
June 14	1	64	112.83	0.260	112.57	0.12	1.500	+0.012	257.58	28.152	0.99614	299850	A.M.
June 14	1	64	112.83	0.260	112.57	0.05	1.517	+0.012	257.60	28.152	0.99614	299880	A.M.
June 14	1	65	112.81	0.260	112.55	0.11	1.517	0.000	257.59	28.152	0.99614	299900	A.M.
June 14	1	66	112.83	0.260	112.57	0.09	1.517	-0.012	257.57	28.152	0.99614	299840	A.M.
June 14	1	67	112.83	0.260	112.57	0.12	1.517	-0.024	257.56	28.152	0.99614	299830	A.M.
June 14	1	84	112.78	0.260	112.52	0.06	1.517	-0.228	257.36	28.159	0.99614	299790	P.M. Readings taken by Lieut. Nazro.
June 14	1	85	112.76	0.260	112.50	0.08	1.500	-0.240	257.33	28.159	0.99614	299810	P.M. Readings taken by Lieut. Nazro.
June 14	1	84	112.72	0.260	112.46	0.08	1.483	-0.228	257.32	28.159	0.99614	299880	P.M. Readings taken by Lieut. Nazro.
June 14	1	84	112.73	0.260	112.47	0.09	1.483	-0.228	257.32	28.159	0.99614	299880	P.M.
June 14	1	84	112.75	0.260	112.49	0.09	1.483	-0.228	257.32	28.129	0.99614	299830	P.M.
June 17	2	62	112.85	0.260	112.59	0.09	1.517	+0.036	257.62	28.149	0.99614	299800	A.M.
June 17	2	63	112.84	0.260	112.58	0.06	1.500	+0.024	257.59	28.149	0.99614	299790	A.M.
June 17	1	64	112.85	0.260	112.59	0.07	1.500	+0.012	257.58	28.149	0.99614	299760	A.M.
June 17	3	77	112.80	0.260	112.54	0.07	1.500	-0.144	257-43	28.157	0.99614	299800	P.M. Readings taken by Mr. Clason.
June 17	3	77	112.77	0.260	112.51	0.08	1.500	-0.144	257.43	28.157	0.99614	299880	P.M. Readings taken by Mr. Clason.
June 17	3	77	112.77	0.260	112.51	0.11	1.500	-0.144	257.43	28.157	0.99614	299880	P.M. Readings taken by Mr. Clason.
June 17	3	77	112.77	0.260	112.51	0.09	1.500	-0.144	257.43	28.157	0.99614	299880	P.M. Readings taken by Mr. Clason.
June 17	3	77	112.78	0.260	112.52	0.08	1.500	-0.144	257 43	28.157	0.99614	299860	P.M. Readings taken by Mr. Clason.
June 18	1	58	112.90	0.265	112.64	0.07	1.500	+0.084	257.65	28.150	0.99614	299720	A.M.
June 18	1	58	112.90	0.265	112.64	0.10	1.500	+0.084	257.65	28.150	0.99614	299720	A.M.
June 18	1	59	112.92	0.265	112.66	0.07	1.483	+0.072	257.62	28.150	0.99614	299620	A.M.
June 18	2	75	112.79	0.265	112.52	0.09	1.483	-0.120	257-43	28.158	0.99614	299860	P.M.
June 18	2	75	112.75	0.265	112.48	0.10	1.483	-0.120	257-43	28.158	0.99614	299970	P.M.
June 18	2	75	112.76	0.265	112.49	0.08	1.483	-0.120	257-43	28.158	0.99614	299950	P.M.
June 20	3	60	112.94	0.265	112.67	0.07	1.517	+0.063	257.65	28.172	0.99614	299880	A.M.
June 20	3	61	112.92	0.265	112.65	0.09	1.517	+0.048	257.63	28.172	0.99614	299910	A.M.
June 20	2	62	112.94	0.265	112.67	0.07	1.517	+0.036	257.62	28.172	0.99614	299850	A.M.
June 20	2	63	112.93	0.265	112.66	0.03	1.517	+0.024	257.61	28.172	0.99614	299870	A.M.
June 20	2	78	133.48	0.265	133.21	0.13	1.450	-0.156	257.36	33.345	0.99627	299840	P.M.
June 20	2	79	133.49	0.265	133.23	0.09	1.500	-0.168	257.40	33.345	0.99627	299840	P.M.
June 20	2	80	133.49	0.265	133.22	0.07	1.500	-0.180	257.39	33.345	0.99627	299850	P.M.
June 20	2	79	133.50	0.265	133.24	0.13	1.483	-0.168	257.39	33.345	0.99627	299840	P.M.
June 20	2	79	133.49	0.265	133.22	0.06	1.483	-0.168	257.38	33.345	0.99627	299840	P.M.
June 20	2	79	133.49	0.265	133.22	0.10	1.483	-0.168	257.38	33.345	0.99627	299840	P.M.
June 21	2	61	133.56	0.265	133.29	0.12	1.533	+0.048	257.65	33.332	0.99627	299890	A.M.
June 21	2	62	133.58	0.265	133.31	0.08	1.533	+0.036	257.64	33.332	0.99627	299810	A.M.
June 21	2	63	133.57	0.265	133.31	0.09	1.533	+0.024	257.63	33.332	0.99627	299810	A.M.
June 21	2	64	133.57	0.265	133.30	0.11	1.533	+0.012	257.61	33.332	0.99627	299820	A.M.
June 21	2	65	133.56	0.265	133.30	0.13	1.533	0.000	257.60	33.332	0.99627	299800	A.M.
June 21	3	80	133.48	0.265	133.21	0.06	1.533	-0.180	257.42	33.330	0.99627	299770	P.M.
June 21	3	81	133.46	0.265	133.19	0.10	1.500	-0.192	257.38	33.330	0.99627	299760	P.M.
June 21	3	82	133.46	0.265	133.20	0.05	1.500	-0.204	257.37	33.330	0.99627	299740	P.M.
June 21	3	82	133.46	0.265	133.20	0.08	1.517	-0.204	257.38	33.330	0.99627	299750	P.M.
June 21	3	81	133.46	0.265	133.19	0.08	1.500	-0.192	257.38	33.330	0.99627	299760	P.M.
June 23	3	89	133.43	0.265	133.16	0.08	1.542	-0.288	257.32	33.345	0.99627	299910	P.M.
June 23	3	89	133.42	0.265	133.15	0.06	1.550	-0.288	257.33	33.345	0.99627	299920	P.M.
June 23	3	90	133.43	0.265	133.17	0.09	1.550	-0.300	257.32	33.345	0.99627	299890	P.M.
June 23	3	90	133.43	0.265	133.16	0.07	1.533	-0.300	257.30	33.345	0.99627	299860	P.M.
June 23	3	90	133.42	0.265	133.16	0.07	1.517	-0.300	257.29	33.345	0.99627	299880	P.M.
June 24	3	72	133.47	0.265	133.20	0.15	1.517	-0.084	257.50	33.319	0.99627	299720	A.M.
June 24	3	73	133.44	0.265	133.17	0.04	1.517	-0.096	257.49	33.319	0.99627	299840	A.M.
June 24	3	74	133.42	0.265	133.16	0.11	1.517	-0.108	257.48	33.319	0.99627	299850	A.M.
June 24	3	75	133.42	0.265	133.16	0.06	1.517	-0.120	257.47	33.319	0.99627	299850	A.M.
June 24	3	76	133.44	0.265	133.18	0.10	1.517	-0.132	257.45	33.319	0.99627	299780	A.M.
June 26	2	86	133.42	0.265	133.15	0.05	1.508	-0.252	257.33	33.339	0.99627	299890	P.M.
June 26	2	86	133.44	0.265	133.17	0.08	1.508	-0.252	257.33	33.339	0.99627	299840	P.M.
June 27	3	73	133.49	0.265	133.22	0.11	1.483	-0.096	257.46	33.328	0.99627	299780	A.M.
June 27	3	74	133.47	0.265	133.20	0.06	1.483	-0.108	257.44	33.328	0.99627	299810	A.M.
June 27	3	75	133.47	0.265	133.21	0.09	1.483	-0.120	257.43	33.328	0.99627	299760	A.M.
June 27	3	75	133.45	0.265	133.19	0.09	1.467	-0.120	257.42	33.328	0.99627	299810	A.M.
June 27	3	76	133.47	0.265	133.20	0.08	1.483	-0.132	257.42	33.328	0.99627	299790	A.M.
June 27	3	76	133.45	0.265	133.19	0.10	1.483	-0.132	257.42	33.328	0.99627	299810	A.M.
June 30	2	85	35.32	135.00	99.68	0.05	1.500	-0.240	193.00	33.274	0.99645	299820	P.M. Mirror inverted.
June 30	2	86	35.34	135.00	99.67	0.06	1.508	-0.252	193.00	33.274	0.99645	299850	P.M. Mirror inverted.
June 30	2	86	35.34	135.00	99.66	0.10	1.508	-0.252	193.00	33.274	0.99645	299870	P.M. Mirror inverted.
June 30	2	86	35.34	135.00	99.66	0.09	1.517	-0.252	193.00	33.274	0.99645	299870	P.M. Mirror inverted.
July  1	2	83	02.17	135.145	132.98	0.07	1.500	-0.216	257.35	33.282	0.99627	299810	P.M. Mirror inverted.
July  1	2	84	02.15	135.145	133.00	0.09	1.500	-0.228	257.34	33.282	0.99627	299740	P.M. Mirror inverted.
July  1	2	86	02.14	135.145	133.01	0.06	1.467	-0.252	257.28	33.311	0.99627	299810	P.M. Mirror inverted.
July  1	2	86	02.14	135.145	133.00	0.08	1.467	-0.252	257.28	33.311	0.99627	299940	P.M. Mirror inverted.
July  2	3	86	99.85	0.400	99.45	0.05	1.450	-0.252	192.95	33.205	0.99606	299950	P.M. Mirror erect.
July  2	3	86	66.74	0.400	66.34	0.03	1.450	-0.252	128.63	33.205	0.99586	299800	P.M. Mirror erect.
July  2	3	86	50.16	0.400	47.96	0.07	1.467	-0.252	96.48	33.205	0.99580	299810	P.M. Mirror erect.
July  2	3	85	33.57	0.400	33.17	0.06	1.450	-0.240	64.32	33.205	0.99574	299870	P.M. Mirror erect.

In the last two sets of June 13, the micrometer was fixed at 113.41 and 112.14 respectively. The image was bisected by the cross-hair, and kept as nearly as possible in this place, meantime counting the number of seconds required for the image of the revolving mirror to complete 60 oscillations. In other words, instead of measuring the deflection, the speed of rotation was measured. In column 7 for these two sets, the numbers 11 and 6 are the differences between the greatest and the smallest number of seconds observed.

In finding the mean value of V from the table, the sets are all given the same weight. The difference between the result thus obtained and that from any system of weights is small, and may be neglected.

The following table gives the result of different groupings of sets of observations. Necessarily some of the groups include others:

Electric light (1 set)	299850
Set micrometer counting oscillations (2)	299840
Readings taken by Lieutenant Nazro (3)	299830
Readings taken by Mr. Clason (5)	299860
Mirror inverted (8)	299840
Speed of rotation, 192 (7)	299990
Speed of rotation, 128 (1)	299800
Speed of rotation, 96 (1)	299810
Speed of rotation, 64 (1)	299870
Radius, 28.5 feet (54)	299870
Radius, 33.3 feet (46)	299830
Highest temperature, 90° Fahr. (5)	299910
Mean of lowest temperatures, 60° Fahr. (7)	299800
Image, good (46)	299860
Image, fair (39)	299860
Image, poor (15)	299810
Frame, inclined (5)	299960
Greatest value	300070
Least value	299650
Mean value	299852
Average difference from mean	60
Value found for π	3.26
Probable error	± 5

Discussion of Errors.

The value of V depends on three quantities D, n, and φ. These will now be considered in detail.

The Distance.

The distance between the two mirrors may be in error, either by an erroneous determination of the length of the steel tape used, or by a mistake in the measurement of the distance by the tape.

The first may be caused by an error in the copy of the standard yard, or in the comparison between the standard and the tape. An error in this copy, of .00036 inch, which, for such a copy, would be considered large, would produce an error of only .00001 in the final result. Supposing that the bisections of the divisions are correct to .0005 inch, which is a liberal estimate, the error caused by supposing the error in each yard to be in the same direction would be only .000014; or the total error of the tape, if both errors were in the same direction, would be 000024 of the whole length.

The calculated probable error of the five measurements of the distance was ±.000015; hence the total error due to D would be at most .00004. The tape has been sent to Professor Rogers, of Cambridge, for comparison, to confirm the result.

The Speed of Rotation.

This quantity depends on three conditions. It is affected, first, by an error in the rate of the standard; second, by an error in the count of the sound beats between the forks; and third, by a false estimate of the moment when the image of the revolving mirror is at rest, at which moment the deflection is measured.

The calculated probable error of the rate is .000016. If this rate should be questioned, the fork can be again rated and a simple correction applied. The fork is carefully kept at the Stevens Institute, Hoboken, and comparisons were made with two other forks, in case it was lost or injured.

In counting the sound beats, experiments were tried to find if the vibrations of the standard were affected by the other fork, but no such effect could be detected. In each case the number of beats was counted correctly to .02, or less than .0001 part, and in the great number of comparisons made this source of error could be neglected.

The error due to an incorrect estimate of the exact time when the images of the revolving mirror came to rest was eliminated by making the measurement sometimes when the speed was slowly increasing, and sometimes when slowly decreasing. Further, this error would form part of the probable error deduced from the results of observations.

We may then conclude that the error, in the measurement of n, was less than .00002.

The Deflection.

The angle of deflection φ was measured by its tangent, tan φ = d/r; d was measured by the steel screw and brass scale, and r by the steel tape.

The value of one turn of the screw was found by comparison with the standard meter for all parts of the screw. This measurement, including the possible error of the copy of the standard meter, I estimate to be correct to .00005 part. The instrument is at the Stevens Institute, where it is to be compared with a millimeter scale made by Professor Rogers, of Cambridge.

The deflection was read to within three or four hundredths of a turn at each observation, and this error appears in the probable error of the result.

The deflection is also affected by the inclination of the plane of rotation to the horizon. This inclination was small, and its secant varies slowly, so that any slight error in this angle would not appreciably affect the result.

The measurement of r is affected in the same way as D, so that we may call the greatest error of this measurement .00004. It would probably be less than this, as the mistakes in the individual measurements would also appear in the probable error of the result.

The measurement of φ was not corrected for temperature. As the corrections would be small they may be applied to the final result. For an increase of 1° F. the correction to be applied to the screw for unit length would be -.0000066. The correction for the brass scale would be +.0000105, or the whole correction for the micrometer would be +.000004. The correction for the steel tape used to measure r would be +.0000066. Hence the correction for tan. φ would be -.000003 t. The average temperature of the experiments is 75°.6 F. 75.6-62.5 = 13.1. -.000003×13.1 = -.00004

Hence φ should be divided by 1.00004, or the final result should be multiplied by 1.00004. This would correspond to a correction of +12 kilometers.

The greatest error, excluding the one just mentioned, would probably be less than .00009 in the measurement of φ.

Summing up the various errors, we find, then, that the total constant error, in the most unfavorable case, where the errors are all in the same direction, would be .00015. Adding to this the probable error of the result, .00002, we have for the limiting value of the error of the final result ±.00017. This corresponds to an error of ±51 kilometers.

The correction for the velocity of light in vacuo is found by multiplying the speed in air by the index of refraction of air, at the temperature of the experiments. The error due to neglecting the barometric height is exceedingly small. This correction, in kilometers, is +80.

Final Result.

The mean value of V from the tables is	299852
Correction for temperature	+12
	------------
Velocity of light in air	299864
Correction for vacuo	80
	------------
Velocity of light in vacuo	299944±51

The final value of the velocity of light from these experiments is then—299940 kilometers per second, or 186380 miles per second.

Objections Considered.

Measurement of the Deflection.

The chief objection, namely, that in the method of the revolving mirror the deflection is small, has already been sufficiently answered. The same objection, in another form, is that the image is more or less indistinct. This is answered by a glance at the tables. These show that in each individual observation the average error was only three ten-thousandths of the whole deflection.

Uncertainty of Laws of Reflection and Refraction in Media in Rapid Rotation.

What is probably hinted at under the above heading is that there may be a possibility that the rapid rotation of the mirror throws the reflected pencil in the direction of rotation. Granting that this is the case, an inspection of Fig. 14 shows that the deflection will not be affected.

In this figure let m m be the position of the mirror when the light first falls on it from the slit at a, and m′ m′ the position when the light returns.

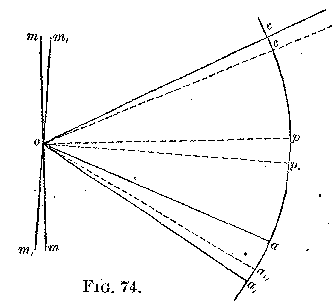
From the axis o draw op op, perpendicular to m m and to m′ m′, respectively. Then, supposing there is no such effect, the course of the axis of the pencil of light would be a o c mirror c o a′. That is, the angle of deflection would be a o a′, double the angle p o p′. If now the mirror be supposed to carry the pencil with it, let o c′ be the direction of the pencil on leaving the mirror m m; i.e., the motion of the mirror has changed the direction of the reflected ray through the angle c o c′. The course would then be a o c, mirror c′ o. From o the reflection would take place in the direction a″, making the angles c′ o p, and p′ o a″ equal. But the angle c o c′ must be added to p o a″, in consequence of the motion of the mirror, or the angle of deviation will be a o a″ + c o c′; or a o a″ + c o c′ = d. (1)

By construction—

c o p′ = p′ o a′ (2)
c′ o p′ = p′ o a″ (3)

Subtracting (3) from (2) we have—

c o p′ - c′ o p′ = p′ o a′ - p′ o a″, or
c o c′ = a′ o a″

Substituting a′ o a″ for c o c′ in (1) we have— a o a″ + a′ o a″ = a o a′ = d.

Or the deflection has remained unaltered.

Retardation Caused by Reflection.

Cornu, in answering the objection that there may be an unknown retardation by reflection from the distant mirror, says that if such existed the error it would introduce in his own work would be only 1/7000 that of Foucault, on account of the great distance used, and on account of there being in his own experiments but one reflection instead of twelve.

In my own experiments the same reasoning shows that if this possible error made a difference of 1 per cent. in Foucault's work (and his result is correct within that amount), then the error would be but .00003 part.

Distortion of the Revolving Mirror.

It, has been suggested that the distortion of the revolving mirror, either by twisting or by the effect of centrifugal force, might cause an error in the deflection.

The only plane in which the deflection might be affected is the plane of rotation. Distortions in a vertical plane would have simply the effect of raising, lowering, or extending the slit.

Again, if the mean surface is plane there will be no effect on the deflection, but simply a blurring of the image.

Even if there be a distortion of any kind, there would be no effect on the deflection if the rays returned to the same portion whence they were reflected.

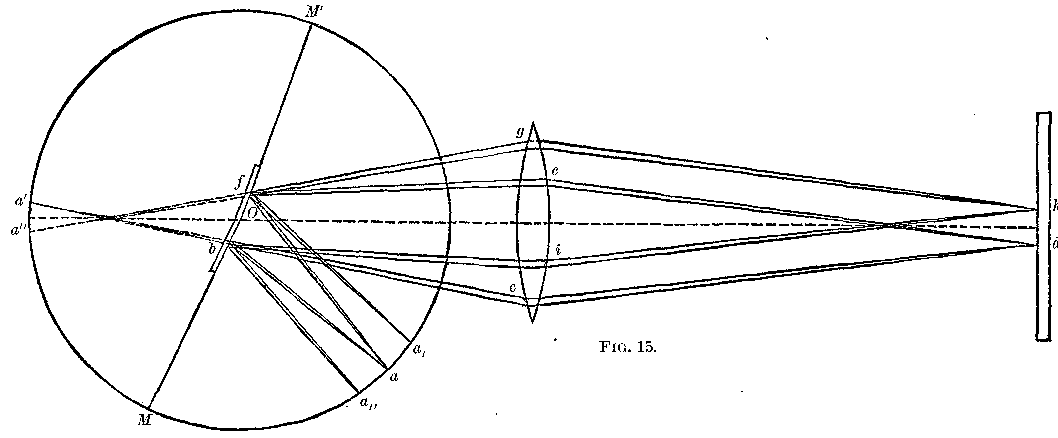
The only case which remains to be considered, then, is that given in Fig. 15, where the light from the slit a, falls upon a distorted mirror, and the return light upon a different portion of the same.

The one pencil takes the course a b c d e f a′, while the other follows the path a f g h i b a′.

In other words, besides the image coinciding with a, there would be two images, one on either side of a, and in case there were more than two portions having different inclinations there would be formed as many images to correspond. If the surfaces are not plane, the only effect is to produce a distortion of the image.

As no multiplication of images was observed, and no distortion of the one image, it follows that the distortion of the mirror was too small to be noticed, and that even if it were larger it could not affect the deflection.

The figure represents the distorted mirror at rest, but the reasoning is the same when it is in motion, save that all the images will be deflected in the direction of rotation.

Imperfection of the Lens.

It has also been suggested that, as the pencil goes through one-half of the lens and returns through the opposite half, if these two halves were not exactly similar, the return image would not coincide with the slit when the mirror was at rest. This would undoubtedly be true if we consider but one-half of the original pencil. It is evident, however, that the other half would pursue the contrary course, forming another image which falls on the other side of the slit, and that both these images would come into view, and the line midway between them would coincide with the true position. No such effect was observed, and would be very unlikely to occur. If the lens was imperfect, the faults would be all over the surface, and this would produce simply an indistinctness of the image.

Moreover, in the latter part of the observations the mirror was inverted, thus producing a positive rotation, whereas the rotation in the preceding sets was negative. This would correct the error mentioned if it existed, and shows also that no constant errors were introduced by having the rotation constantly in the same direction, the results in both cases being almost exactly the same.

Periodic Variations in Friction.

If the speed of rotation varied in the same manner in each revolution of the mirror, the chances would be that, at the particular time when the reflection took place, the speed would not be the same as the average speed found by the calculation. Such a periodic variation could only be caused by the influence of the frame or the pivots. For instance, the frame would be closer to the ring which holds the mirror twice in every revolution than at other times, and it would be more difficult for the mirror to turn here than at a position 90° from this. Or else there might be a certain position, due to want of trueness of shape of the sockets, which would cause a variation of friction at certain parts of the revolution.

To ascertain if there were any such variations, the position of the frame was changed in azimuth in several experiments. The results were unchanged showing that any such variation was too small to affect the result.

Change of Speed of Rotation.

In the last four sets of observations the speed was lowered from 256 turns to 192, 128, 96, and 64 turns per second. The results with these speeds were the same as with the greater speed within the limits of errors of experiment.

Bias.

Finally, to test the question if there were any bias in taking these observations, eight sets of observations were taken, in which the readings were made by another, the results being written down without divulging them. Five of these sets are given in the "specimen," pages 133-134.

It remains to notice the remarkable coincidence of the result of these experiments with that obtained by Cornu by the method of the "toothed wheel."

Cornu's result was 300400 kilometers, or as interpreted by Helmert 299990 kilometers. That of these experiments is 299940 kilometers.

Postscript.

The comparison of the micrometer with two scales made by Mr. Rogers, of the Harvard Observatory, has been completed. The scales were both on the same piece of silver, marked "Scales No. 25, on silver. Half inch at 58° F., too short .000009 inch. Centimeter at 67° F., too short .00008 cm."

It was found that the ratio .3937079 could be obtained almost exactly, if, instead of the centimeter being too short, it were too long by .00008 cm. at 67°.

On this supposition the following tables were obtained. They represent the value of one turn of the micrometer in millimeters.

Table 1 is the result from centimeter scale.

Table 2 is the result from half-inch scale.

Table 3 is the result from page 31.

It is seen from the correspondence in these results, that the previous work is correct.

	(1)	(2)	(3)
From 0 to	13	.99563	.99562	.99570
	25	.99562	.99564	.99571
	38	.99560	.99572	.99576
	51	.99567	.99578	.99580
	64	.99577	.99586	.99585
	76	.99582	.99590	.99592
	89	.99590	.99598	.99601
	102	.99596	.99608	.99605
	115	.99606	.99614	.99615
	128	.99618	.99622	.99623
	140	.99629	.99633	.99630

End of the Project Gutenberg EBook of Experimental Determination of the
Velocity of Light, by Albert A. Michelson

*** END OF THIS PROJECT GUTENBERG EBOOK VELOCITY OF LIGHT ***

***** This file should be named 11753-h.htm or 11753-h.zip *****
This and all associated files of various formats will be found in:
        http://www.gutenberg.net/1/1/7/5/11753/

Page images provided by Case Western Reserve University's Digital
Preservation Department


Updated editions will replace the previous one--the old editions
will be renamed.

Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties.  Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark.  Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission.  If you
do not charge anything for copies of this eBook, complying with the
rules is very easy.  You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research.  They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks.  Redistribution is
subject to the trademark license, especially commercial
redistribution.



*** START: FULL LICENSE ***

THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK

To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License (available with this file or online at
http://gutenberg.net/license).


Section 1.  General Terms of Use and Redistributing Project Gutenberg-tm
electronic works

1.A.  By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement.  If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.

1.B.  "Project Gutenberg" is a registered trademark.  It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement.  There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement.  See
paragraph 1.C below.  There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works.  See paragraph 1.E below.

1.C.  The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works.  Nearly all the individual works in the
collection are in the public domain in the United States.  If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed.  Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work.  You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.

1.D.  The copyright laws of the place where you are located also govern
what you can do with this work.  Copyright laws in most countries are in
a constant state of change.  If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work.  The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.

1.E.  Unless you have removed all references to Project Gutenberg:

1.E.1.  The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:

This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever.  You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.net

1.E.2.  If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges.  If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.

1.E.3.  If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder.  Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.

1.E.4.  Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.

1.E.5.  Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.

1.E.6.  You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form.  However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.net),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form.  Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.

1.E.7.  Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.

1.E.8.  You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that

- You pay a royalty fee of 20% of the gross profits you derive from
     the use of Project Gutenberg-tm works calculated using the method
     you already use to calculate your applicable taxes.  The fee is
     owed to the owner of the Project Gutenberg-tm trademark, but he
     has agreed to donate royalties under this paragraph to the
     Project Gutenberg Literary Archive Foundation.  Royalty payments
     must be paid within 60 days following each date on which you
     prepare (or are legally required to prepare) your periodic tax
     returns.  Royalty payments should be clearly marked as such and
     sent to the Project Gutenberg Literary Archive Foundation at the
     address specified in Section 4, "Information about donations to
     the Project Gutenberg Literary Archive Foundation."

- You provide a full refund of any money paid by a user who notifies
     you in writing (or by e-mail) within 30 days of receipt that s/he
     does not agree to the terms of the full Project Gutenberg-tm
     License.  You must require such a user to return or
     destroy all copies of the works possessed in a physical medium
     and discontinue all use of and all access to other copies of
     Project Gutenberg-tm works.

- You provide, in accordance with paragraph 1.F.3, a full refund of any
     money paid for a work or a replacement copy, if a defect in the
     electronic work is discovered and reported to you within 90 days
     of receipt of the work.

- You comply with all other terms of this agreement for free
     distribution of Project Gutenberg-tm works.

1.E.9.  If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark.  Contact the
Foundation as set forth in Section 3 below.

1.F.

1.F.1.  Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection.  Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.

1.F.2.  LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees.  YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH F3.  YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.

1.F.3.  LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from.  If you
received the work on a physical medium, you must return the medium with
your written explanation.  The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund.  If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund.  If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.

1.F.4.  Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS', WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTIBILITY OR FITNESS FOR ANY PURPOSE.

1.F.5.  Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law.  The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.

1.F.6.  INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.


Section  2.  Information about the Mission of Project Gutenberg-tm

Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers.  It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.

Volunteers and financial support to provide volunteers with the
assistance they need, is critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come.  In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation web page at http://www.pglaf.org.


Section 3.  Information about the Project Gutenberg Literary Archive
Foundation

The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service.  The Foundation's EIN or federal tax identification
number is 64-6221541.  Its 501(c)(3) letter is posted at
http://pglaf.org/fundraising.  Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.

The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations.  Its business office is located at
809 North 1500 West, Salt Lake City, UT 84116, (801) 596-1887, email
[email protected].  Email contact links and up to date contact
information can be found at the Foundation's web site and official
page at http://pglaf.org

For additional contact information:
     Dr. Gregory B. Newby
     Chief Executive and Director
     [email protected]

Section 4.  Information about Donations to the Project Gutenberg
Literary Archive Foundation

Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment.  Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.

The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States.  Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements.  We do not solicit donations in locations
where we have not received written confirmation of compliance.  To
SEND DONATIONS or determine the status of compliance for any
particular state visit http://pglaf.org

While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.

International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States.  U.S. laws alone swamp our small staff.

Please check the Project Gutenberg Web pages for current donation
methods and addresses.  Donations are accepted in a number of other
ways including including checks, online payments and credit card
donations.  To donate, please visit: http://pglaf.org/donate


Section 5.  General Information About Project Gutenberg-tm electronic
works.

Professor Michael S. Hart is the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone.  For thirty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.

Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included.  Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.

Each eBook is in a subdirectory of the same number as the eBook's
eBook number, often in several formats including plain vanilla ASCII,
compressed (zipped), HTML and others.

Corrected EDITIONS of our eBooks replace the old file and take over
the old filename and etext number.  The replaced older file is renamed.
VERSIONS based on separate sources are treated as new eBooks receiving
new filenames and etext numbers.

Most people start at our Web site which has the main PG search facility:

     http://www.gutenberg.net

This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.

EBooks posted prior to November 2003, with eBook numbers BELOW #10000,
are filed in directories based on their release date.  If you want to
download any of these eBooks directly, rather than using the regular
search system you may utilize the following addresses and just
download by the etext year. For example:

     http://www.gutenberg.net/etext06

    (Or /etext 05, 04, 03, 02, 01, 00, 99,
     98, 97, 96, 95, 94, 93, 92, 92, 91 or 90)

EBooks posted since November 2003, with etext numbers OVER #10000, are
filed in a different way.  The year of a release date is no longer part
of the directory path.  The path is based on the etext number (which is
identical to the filename).  The path to the file is made up of single
digits corresponding to all but the last digit in the filename.  For
example an eBook of filename 10234 would be found at:

     http://www.gutenberg.net/1/0/2/3/10234

or filename 24689 would be found at:
     http://www.gutenberg.net/2/4/6/8/24689

An alternative method of locating eBooks:
     http://www.gutenberg.net/GUTINDEX.ALL