Dynamic Hydropower
The ‘suction turbine’ or ‘jet turbine’ of Viktor Schauberger
Hydropower
engineering, up to this day, is almost esclusively concerned with two variables,
one being the altitude differential between head water and turbine and the other
the quantity of water that can be brought to flow through the turbines.
A
third important variable, the velocity of flow of water, is generally not
thought to be important. It is taken into consideration only as the velocity
resulting from the release of water pressure connected to and dependent on
altitude differential but not as an important factor in its own right. In fact,
current design of hydropower facilities normally excludes utilization of the
dynamic energy potential inherent in the free flow of water. A dam destroys this
natural energy potential by bringing the water from its dynamic state of flow to
a static state, a complete absence of motion.
If we study the writings of
Viktor Schauberger and Ludwig Herbrand, we find that the energy inherent in the
free and unhindered flow of water may be potentially much greater than that
obtainable from the exclusive use of pressure resulting from altitude
differential.
A normal flow of water rather than an altitude-induced
pressure, has been used in mills and old blacksmith hammerworks of the
pre-industrial era.
Schauberger
In recent times, it was Viktor Schauberger, the austrian
inventor and genial observer of nature’s ways who first advocated the use of
increased water velocity rather than water pressure for the production of
hydroelectric power. He obtained a patent for what he termed a jet turbine
(Strahlturbine) as early as the year 1930. (1)
The principles used by
Schauberger in order to increase water velocity were the jet configuration of
the water inlet pipe and the promotion, by spiral ribbings on the inside of the
jet, of a vortex motion of the water.
Schauberger’s patent actually gives
us two very important clues to innovative changes in hydropower
technology.
The first one is, that a pipe configured as a funnel or jet
will increase the velocity of the water’s flow by restricting the space
available in which the water may flow. This increase in velocity is especially
great if the funnel or jet allows the water to form a characteristic flow
pattern known as a vortex. This vortex pattern itself has a tendency, quite
separate from the jet-effect, to increase the velocity of the water, to decrease
its temperature and to augment the water’s density.
The second innovation
proposed by Schauberger is a revolutionary design of the turbine, obtaining
rotation at very high speeds and at the same time avoiding the usual
difficulties of cavitation found in normal high speed turbine designs. In fact
Schauberger’s turbine wheel is of conical shape, with blades spiralling down the
surface of the cone in a corkscrew pattern, and it is located in the center of
the jet of water. The corkscrew turbine wheel parts the flow of water, takes up
the water’s dynamic energy and lets the flow continue without major disruption.
Turbines of current design ‘hack’ the water into thousands of destructive
counter flows and cross vortices, thus wasting much of the available energy and
causing the common problem of cavitation, a super fast corrosion and destruction
of turbine blade material.
Here is the description of this new type of
turbine as given in Schauberger’s patent number 117 749:
'The subject of
the invention is a hydropower machine, which utilizes the living energy of a jet
of water for the purpose of power generation.
According to the invention,
the turbine wheel is a cone with corkscrew-like blades. The cone is aligned with
its axis in the direction of the axis of the jet. In this way the jet of water
is split and diverted out of its course and thus gives its whole living energy
to the spinning cone in a way that, providing the lenght of the cone and the
width of its base are in a correct relation to each other and provided the
blades are set at the correct angle, these parameters depending on the speed of
the water jet, the water will flow out of the machine without
agitation.
The illustration is an approximate schematic representation of
the invention.
The spinning cone, which is aligned with its axis (1) in
the direction of the water jet leaving the jet pipe (2), is made up of blades
(3) in the form of a corkscrew.
 The
ends (4) of these blades (3) are bent somewhat upwards against the direction of
the arriving water jet in order to cause a diversion of the jet and to transfer
as much as possible of the living energy of the jet to the spinning
cone.
The
ends (4) of these blades (3) are bent somewhat upwards against the direction of
the arriving water jet in order to cause a diversion of the jet and to transfer
as much as possible of the living energy of the jet to the spinning
cone.
On the inside of the jet pipe (2) there are screw-like ribs (5)
promoting a spin, which according to actual observations increase the speed of
the water jet and the efficiency of the machine.
PATENT CLAIMS:
- A jet turbine, distinguished by the fact that in the path of the water jet
and aligned with its axis so as to split the jet, there is a turbine wheel in
the form of a cone, the surface of which is formed of corkscrew-like blades.
- A jet turbine according to claim 1, distinguished by a jet pipe (2) with
ribs (5) slanted in the direction of spin of the turbine wheel.’ This patent
was applied for in 1926 and granted in 1930. It seems that Schauberger
actually used a small turbine of this design in a stream of water near the
forest wardens’ building during those years, but no reliable records are
available. (2)
Herbrand
Another instance of the use of the dynamic powers of flowing
water has been documented by Ludwig Herbrand, a german engineer who as a student
in the mid 1930’s was called to evaluate and calculate the parameters of some
generators and exciter units that had recently been installed in the Rheinfelden
power station, as well as to design electrical overload protection and relevant
switching mechanisms for these generators. He was also required to compare the
generators with those of another power station that had been described in an
article of a specialized magazine.
Much to the dismay of the then young
and inquisitive engineering student, it seemed that the generators under
examination were supplying more electrical energy than they should have,
according to accepted theory. One of the generators of the Rheinfelden power
plant, with 50 cubic meters of water per second and an altitude differential of
only one meter supplied just as much power as a generator in near
Ryburg-Schwšrstadt, which had a capacity of 250 cubic meters of water per second
and an altitude differential from head waters to turbine of 12 meters!
(3)
That fact was confirmed by prof. Finzi, the designer of the turbines
and generators, saying to young Herbrand:
"Do not worry about this. It
is correct. The generator has been working without problems for some time now.
Make the calculations backwards and you will see for yourself. We are electrical
engineers. Why, those other problems are not ours to solve, we leave them to the
water people. We have repeated our measurements and the generator’s yield of
power is exactly as specified. The only thing is - no one knows about this."
(4)
Herbrand was soon drafted into the army and World War II did not
allow him to pursue the matter further. Only much later, in the 1970s and 1980s,
Herbrand came back to the calculations made for his engineering exams and tried
- so far without success - to interest industry and government in this different
and more efficient use of hydropower.
Technical facts
I shall attempt to delineate here the technical facts,
using calculations that are based on accepted formulas and physical
considerations confirmed by actual experiment, to show that with a different
approach to hydropower engineering, we could obtain significantly more
electrical power than is being extracted from hydro resources today, with
simpler machinery and less expenditure, as well as less disturbance to the
environment.
As mentioned above, current hydropower engineering works
with water pressure, obtained as a result of the altitude differential between
head waters and location of the turbine. This pressure, when released through
the turbine, results in a momentary acceleration of the water and thus in a
certain velocity of the water jet. This velocity is calculated with the formula
v = Sqrt 2 g hv being the velocity, g the gravitational
acceleration of the earth (9.81 m/sec2) and h the altitude differential measured
in meters.
Example: An altitude of 12 m results in a velocity of Sqrt 2 .
9.81 . 12 = 15.3 m/sec.
The progression of velocity in relation to
altitude differential is shown in the following table.
altitude diff. 12 m 24 m 36 m 8 m 60 m
velocity 15.3 m/sec 21.7 m/sec 26.6 m/sec 30.7 m/sec 34.3 m/sec
altitude diff. 72 m 84 m 96 m 108 m 120 m
velocity 37.6 m/sec 40.6 m/sec 43.4 m/sec 46 m/sec 48.5 m/sec
altitude diff. 132 m 144 m 156 m 168 m 180 m
velocity 50.9 m/sec 53.15 m/sec 55.3 m/sec 57.4 m/sec 59.4 m/sec
altitude diff. 192 m 204 m 216 m 228 m 240 m
velocity 61.4 m/sec 63.3 m/sec 65.1 m/sec 66.9 m/sec 68.6 m/sec
These values are rendered graphically
below.
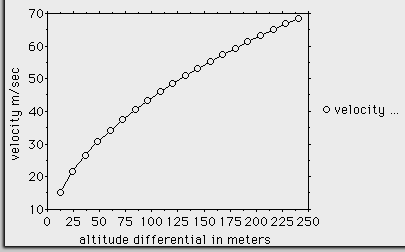
We see
that the curve of velocity at first increases more steeply and then tends to
flatten with higher altitude differentials.
Let us now examine the energy
output in kilowatt with increasing altitude differential.

The
increase of energy output is linear, as shown in the graphic above.
Calculation
The electric energy that can be obtained from water is
calculated on the basis of the velocity of flow and the mass of the water, i.e.
magnitude of flow measured in cubic meters per second, according to the
formula
E kin = m/2 x v 2 (kw)
An example, assuming a velocity of 25 m/sec and a mass of 5 cubic meters per
second:
5 / 2 = 2.5 x 25 x 25 = 1562.5 kw
For the purpose of comparison, here are some further examples (assuming a
small constant flow of water, only 2 cubic meters per second):
velocity 15 m/sec 20 m/sec 25 m/sec 30 m/sec 35 m/sec
energy 225 kw 400 kw 625 kw 900 kw 1225 kw
velocity 40 m/sec 45 m/sec 50 m/sec 55 m/sec 60 m/sec
energy 1600 kw 2025 kw 2500 kw 3025 kw 3600 kw
velocity 65 m/sec 70 m/sec 75 m/sec 80 m/sec 85 m/sec
energy 4225 kw 4900 kw 5625 kw 6400 kw 7225 kw
velociyt 90 m/sec 95 m/sec 100 m/sec 105 m/sec 110 m/sec
energy 8100 kw 9025 kw 10000 kw 11025 kw 12100 kw
These figures show, that a doubling
of velocity quadruples the power output, a threefold increase of velocity leads
to a ninefold increase of power output. In other words, we have an exponential
increase. The curve of energy increase plotted against water velocity is shown
in this third graphic.
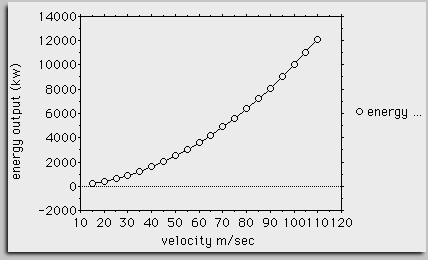
The
graphic representation makes it clear, that a velocity increase brings
progressively larger increases of energy. Therefore, the higher the velocity of
the water, the greater the overall efficiency of the power plant!
For the
purpose of utilizing hydropower for generating electrical energy, it is however
quite irrelevant whether the velocity of the water is the result of pressure
obtained through altitude differential or whether it is obtained in some other
way, such as encouraging the natural tendency of water to flow. And it seems
that we can increase the velocity of flow of water almost at will.
How to increase electrical output
There are two basic variables in
hydropower engineering that determine electrical output. They are the amount of
water available and the velocity of flow. The first variable, the amount of
water available, depends very much on location and is generally not subject to
increase by human intervention.
It is the second variable, the velocity
of the water’s flow, which can be manipulated in many ways. Apart from
increasing water pressure, which is a comparatively inefficient way to increase
flow velocity, this parameter can be influenced by other, more simple and more
cost effective engineering solutions.
It is a common principle in
rocketry to increase the velocity of flow of the hot exhaust gases by a
restriction of the path of flow of these gases. This is called the jet principle
and has been used successfully for decades.
The same principle can be
used to increase the velocity of a flow of water, such as a river. In fact,
where a river is forced, by the natural configuration of terrain, to flow
through a narrow gorge, the velocity at the narrowest point is much higher than
it is before and after the river’s passage through the gorge. This effect can be
utilized by finding a natural gorge or by artificially narrowing a river’s bed
so as to bring about an increase in water velocity.
Another way to
increase velocity of flow in water is to promote the formation of a longitudinal
vortex. This is a rolling or spinning motion, the axis of which coincides with
the direction of flow of the water. Such vortices have the property of causing
an increase of the velocity of flow, and a contraction of the diameter of the
space needed by the body of water. They also cause a lowering of the water’s
temperature and thus an increase in its density. (The highest specific density
of water is reached at a temperature of + 4º C.)
Water has a natural
tendency to form vortices, especially if its flow is accelerated by some
external influence such as gravity. We can observe this by noting the swirl with
which a full bathtub or sink or any other container full of water empties, if
the water is forced to flow through a pipe connected to a hole in the bottom of
the container. But even a simple water faucet, releasing a flow of water, will
show this same phenomenon if the water flows relatively undisturbed, without
bubbles or agitation. As the water picks up speed, it forms a distinctly
funnel-shaped vortex right before our eyes.
A confirmation of this
tendency of vortices to increase water velocity (or in other words to decrease
resistance to the water’s flow) comes from experiments performed in 1952 at the
Technical College in Stuttgart by Prof. Franz Pšpel and Viktor
Schauberger.
The experiments were performed with pipes of different
materials and different shapes, to determine if either materials or shapes had
an influence on the resistance of the flow of water in pipes.
It seems
that best results were achieved with copper pipes, and that this material caused
less resistance to the water’s flow than even the smooth glass pipes used as
comparison. But the most important datum emerging from these experiments is,
that by using a certain spiral configured pipe, based on the form of the kudu
antelope’s horn, the friction in this pipe decreased with an increase in
velocity and at a certain point, the water flowed with a negative resistance.
(5)
Theory and practice
The best theory is not worth the paper it is written
on, if it cannot be put into practice. We shall therefore examine the practical
utilization of these principles in hydropower engineering.
The object is
to increase the velocity of the flow of water to such a degree that the
resulting jet will release more kinetic energy than conventional utilization of
water pressure achieved with comparable means.
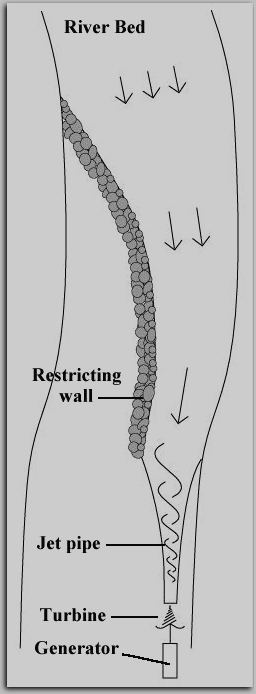 Step
1:
Step
1:
As a first step, a river’s normal flow is brought to higher velocity
by the expedient of a wall that gradually restricts the river’s bed. This will
increase the normal velocity of flow of 2 - 5 m/sec to a sizeable 10 - 15
m/sec.
Step 2:
At this point, in order to further increase
velocity, we must provide a channel of flow that more closely resembles the
shape of a natural vortex.We do this by channelling the already swiftly flowing
water at the narrowest point of the river bed into an approximately round
‘funnel’ or ‘jet-pipe’ which gradually further restricts the diameter of the
water’s channel of flow and thereby causes a further increase in
velocity.
In order to aid this process, we can promote the formation of a
vortex in the funnel or jet-pipe which will ensure that the water exits the jet
at a considerable velocity. This is done either by spiral ribs on the inside of
the jet-pipe as proposd by Schauberger, or by forming the whole pipe in a
slightly ‘corkscrew’ configuration.
Installing a turbine and generator at
the release point of the water jet, preferably of the design proposed by
Schauberger, will now provide an output of electrical power much higher than
that achieved by comparable means in the conventional way.
Where step 1
is not practicable because of the river being too small, or where we simply want
to adapt existing power plants to utilize the dyna;ic energy of water flow, step
2 can still be profitably combined with current small hydropower plant design,
by altering the shape of the penstock to a funnel or jet-pipe configuration,
thus obtaining part of the velocity increase from normal use of gravity and
another part through the specific action of the jet effect and the vortex
flow.
No theoretical limitation
Are there limits to how fast a water-jet can
be made to flow? This is a question we should obviously ask ourselves before
embarking on this kind of project.
It seems that theoretically there are
no limitations, as long as the vortex mode of flow is used. If water is forced
to flow in straight pipes, resistance increases with the increase of velocity.
Not so when we allow the water to flow at its natural mode, accomodating the
resulting vortex in our pipe design. In this case, resistance can be very low
and even negative, as shown by the experiments performed in
Stuttgart.
For purposes of estimating the potential benefits of using the
dynamic powers inherent in the flow of water, we can conservatively assume that
we should be able to obtain, without particular difficulties, velocities between
40 and 50 m/sec. This is an estimation based on the observation of Herbrand that
at the Rheinfelden power plant a velocity of 35 m/sec was achieved.
We
can see from the above statistical tables that 45 m/sec of velocity are
equivalent to an altitude differential of more than 100 meters. And assuming
that we have a flow of water of 10 cbm/sec, we can predict (at v = 45 m/sec) an
energy output of 10 megawatt. This is a considerable amount of power and it can
be obtained almost anywhere along the normal course of a river, without the
costly and environmentally questionable practice of constructing a dam and a man
made lake to obtain 100 meters of altitude differential.
If it is true
that the water’s velocity of flow can be increased almost at will and with
comparatively simple means at a fraction of the cost of current hydropower
designs, someone might ask: Why are we not using this obviously superior
method?
Fixed ideas and the ‘law of conservation of energy’
It is very hard to
un-learn something one studied and especially if what was learned was then
needed to pass an examination. The weight of socalled ‘natural laws’ brought to
bear to support these doctrines makes it even more difficult for any one person
to stand up and say ‘hey, we have overlooked something here!’
Of course
‘everybody knows’ that water has to be pressurized if we are to use it for
hydroelectric power generation. And everybody knows as well, that the technology
of hydropower engineering has been well in hand since the turn of the century.
So why bother to look any further?
Not so Ludwig Herbrand. He has fought
an unceasing battle for more than 20 years now, to obtain recognition for this
new technology. Literally hundreds of letters to government and industry, as
well as international institutions with just so many negative replies, more or
less politely telling him that his proposals are not welcome.
It is
difficult to break through this barrier of ‘knowledge’, especially when the
experts think they see a violation of the law of conservation of energy.
Conservation of energy is invoked when calculations do not seem to permit a
higher energy output. But in this case we have a factor that has been neglected
in our calculations, not a violation of conservation laws.
Water is an accumulator of energy
There is some evidence that the
decrease of water temperature that is a consequence of vortex motion provides
the energy to the water that we then see as kinetic energy in the form of
increased water velocity. In this way a vortex would transform heat (which is
random molecular motion) into dynamic energy (which is motion in a certain
direction). Schauberger stressed the fact that water could store enormous
amounts of energy by being heated up. He states in an article about the Danube
river that in order to warm up 1 cubic meter of water by only 0.1 degree C, one
needs about 42,700 kgm of energy, saying that this goes to show the enormous
energies that are bound when water is heated up and are released when water
cools down. (6)
Thermodynamics, as taught in our schools and universities
does not allow for such a two-way transformation of heat at low temperature
differentials. Thermodynamics is based on observation of steam machines and has
little to do with nature, although some insist that the socalled laws of
thermodynamics are ‘natural laws’. Nevertheless, thermodynamics is not able to
explain certain natural phenomena. (7)
In calculations of electrical
power yield, velocity is not considered separately but as a result only and
exclusively of altitude differential. That is like saying, there is no other way
of achieving water velocity than pressure. It may be the way the experts
calculate, but physical reality is different. Water velocity, as we have seen,
is not exclusively linked to pressure but may be achieved with different
means.
Thus the correct way to calculate is to start from velocity and
arrive at the power output. Altitude differential and the velocity equivalent as
calculated in the formula given above are a special case, not the general
rule.
We must distinguish between the pressure-induced velocity
equivalent and the natural velocity of flowing water. That is to say we must
distinguish between gravity and inertia. These two forces are similar in their
effects but they are nevertheless two distinctly different forces. This article
does not allow a detailed examination of the physical forces involved. For those
who are interested in this subject, I would like to refer to an article I have
written on the basics of physics in EXPLORE! in 1992. (8)
I hope that
this article may contribute to overcoming the ‘knowledge barrier’, the various
‘everybody knows’ in the field of hydro engineering. To anyone wishing to
utilize the dynamic powers of water I recommend a study of the writings of
Viktor Schauberger, the great master of hydro engineering who remained an
outsider to official science all of his life, because his views were so
radically different from those of the professors of his time.
Josef
Hasslberger
Rome, December 1993
References:
- Patent granted to Viktor Schauberger by Austrian Patent Office, number 117
749 of 10 May 1930
- Implosion nr. 58, pg 31 article (unsigned) ‘Kann Energie wachsen?’
- Hasslberger, Josef ‘Understanding Water Power’ EXPLORE! Vol. 4 number 1,
1993
- Herbrand, Ludwig ‘Das Geheimnis der Wasserkraft’, 1. Nov. 1990, S. 9
- Alexandersson, Olof ‘Living Water’ Gateway Books, Bath, UK
- Schauberger, Viktor ‘Das Problem der Donauregulierung’ in Implosion nr. 23
- Hasslberger, Josef ‘A new Beginning for Thermodynamics’ EXPLORE! Vol. 4
number 5, 1993
- Hasslberger, Josef ‘Physics - At the End of a Blind Alley?’ EXPLORE! Vol.
3 number 5, 1992

 The
ends (4) of these blades (3) are bent somewhat upwards against the direction of
the arriving water jet in order to cause a diversion of the jet and to transfer
as much as possible of the living energy of the jet to the spinning
cone.
The
ends (4) of these blades (3) are bent somewhat upwards against the direction of
the arriving water jet in order to cause a diversion of the jet and to transfer
as much as possible of the living energy of the jet to the spinning
cone.


 Step
1:
Step
1: