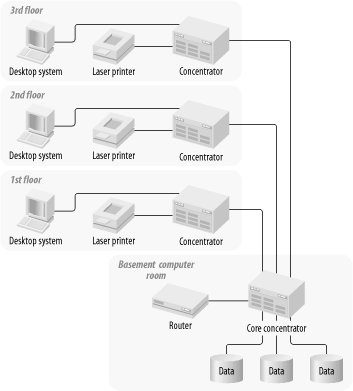
Figure 2-1. A simple LAN without redundancy
An obvious technique for improving reliability is to duplicate key pieces of equipment, as in the example of the heavily used bridge between two densely populated areas. The analogy shows two potential benefits to building a second bridge. First, if the first bridge is damaged or needs maintenance, the second bridge will still be there to support the traffic. Second, if the roads leading to these bridges are well planned, then it should be possible to balance their traffic loads. This will improve congestion problems on these major routes.
Exactly the same is true of key network devices. If you duplicate the device, you can eliminate single points of failure. Using redundancy can effectively double throughput in these key parts of the network. But, just as in the highway example, neither benefit is assured. Duplicating the one device that never fails and never needs maintenance won't improve anything. And throughput is only increased if the redundant equipment is able to load-share with the primary equipment.
These two points are also clear when talking about the car bridge. It may be difficult to justify spending large amounts of money on a second bridge just because the first one might one day be flooded out, unless the danger of this failure is obvious and pressing. Bridges are expensive to build. Besides, if high water affects the first bridge, it might affect the second bridge as well. In short, you have to understand your expected failure modes before you start spending money to protect against them.
Similarly, if the access roads to the second bridge are poorly designed, it could be that nobody will use it. If it is awkward to get there, people will balance the extra time required to cross the heavily congested first bridge against the extra time to get to the under-used second bridge.
Finally, if the first bridge is almost never seriously congested, then the financial commitment to build a second one is only justified if there is good reason to believe that it will be needed soon.
All of these points apply to networks as well. If a network is considered unreliable, then implementing redundancy may help, but only if it is done carefully. If there is a congestion problem, then a redundant path may help, but only if some sort of load balancing is implemented between the old and new paths. If the problem is due to component failure, then the redundancy should focus on backing up those components that are expected to fail. If it is being built to handle future growth, then the growth patterns have to be clearly understood to ensure that the enhancements are made where they are most needed.
Redundancy also helps with maintenance. If there is backup equipment in a network, then the primary components can be taken offline without affecting the flow of traffic. This can be particularly useful for upgrading or modifying network hardware and software.
Clearly some careful thought is required to implement redundancy usefully. There are a number of general guidelines to help with this, but I will also discuss instances where it might be a good idea to ignore these guidelines.
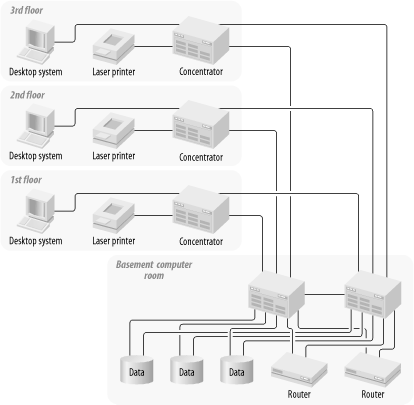
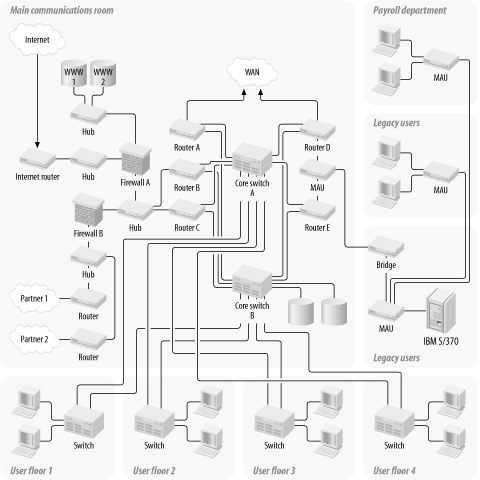
The first rule of thumb is to duplicate all Core equipment, but don't back up a backup.[1] Figure 2-1 and Figure 2-2 show a typical small part of a large LAN without and with redundancy, respectively. In Figure 2-2 the Core concentrator and the router have both been duplicated. There is even a second NIC installed in each of the servers. What has been accomplished in doing this?
[1] As I will discuss later, there are actually cases where it is useful to back up a backup. If there are good reasons to expect multiple failures, or if the consequences of such a multiple failure would be catastrophic, it is worth considering. However, later in this chapter I show mathematically why it is rarely necessary.

For the time being, I will leave this example completely generic. The LAN protocols are not specified. The most common example would involve some flavor of Ethernet. In this case the backup links between concentrators will all be in a hot standby mode (using Spanning Tree). This is similar to saying that the second highway bridge is closed unless the first one fails. So there is no extra throughput between the concentrators on the user floors and the concentrators in the computer room. Similarly, the routers may or may not have load-sharing capability between the two paths. So it is quite likely that the network has gained no additional bandwidth through the Core. Later, I go into some specific examples that explore load sharing as well as redundancy, but in general there is no reason to expect that it will work this way.
In fact, for all the additional complexity in this example, the only obvious improvement is that the Core concentrator has been eliminated as a single point of failure. This may be an important improvement. But it could also prove to be a lot of money for no noticeable benefit. And if the switchover from the primary to secondary Core concentrators is a slow or manual process, the network may see only a slight improvement in overall reliability. You would have to understand your expected failure modes before you could tell how useful this upgrade has been.
This example looks like it should have been a good idea, but maybe it wasn't. Where did it go wrong? Well, the first mistake was in assuming that the problem could be solved simply by throwing gear at it. In truth, there are far too many subtleties to take a simple approach like this. One can't just look at physical connectivity. Most importantly, be very careful about jumping to conclusions. You must first clearly understand the problem you are trying to solve.
Consider this same network in more detail. Besides having a physical drawing, there has to be a network-layer drawing. This means that I have to get rid of some of the generality. But specific examples are often useful in demonstrating general principles.
Figure 2-3 shows the same network at Layer 3. I will assume that everything is Ethernet or Fast Ethernet. I will also assume a TCP/IP network. The simplest nontrivial example has two user VLANs and one server VLAN.
I talk about VLANs, routers, and concentrators in considerable detail in Chapter 3 and Chapter 4. But for now it is sufficient to know that a VLAN is a logical region of the network that can be spread across many different devices. At the network layer (the layer where IP addresses are used to contact devices), VLANs are composed of groups of devices that are all part of the same subnet (assuming IP networking for now). Getting a packet from one VLAN to another is the same, then, as sending it from one IP subnet to another. So the traffic needs to pass through a router.
There are two groups of users, divided into two VLANs. These users may be anywhere on the three floors. All of the servers, however, are on a separate server VLAN. So, every time a user workstation needs to communicate with a server, it has to send the packet first to the router, which then forwards the packet over to the server.
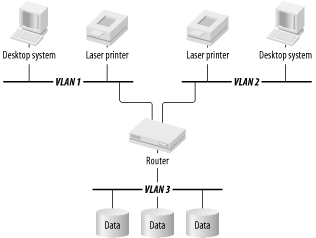
Notice in Figure 2-3 how different the diagram looks at the network layer than it did at the physical layer. It is the same network, but looked at in another complementary way. There are many different ways to implement the same physical network logically. This subject will be discussed in depth later in this book because exploiting this flexibility is what network design is all about.
In Figure 2-3 there are two user VLANs and one server VLAN. These two user segments are spread throughout the three physical floors in Figure 2-1 and Figure 2-2. So the users shown in Figure 2-3 could be anywhere in the building. The server VLAN exists only in the basement and only supports the servers. In theory there is no reason why this VLAN could not also be distributed among all of the concentrators, as the user VLANs were. But in this example, assume that the servers have been given their own VLAN.
Data has to pass through the router to get from one VLAN to another. In the physical-layer diagram (Figure 2-1), the router looks almost like just another server. It is much harder to see why it should have a backup. But in the network-layer diagram (Figure 2-3), it becomes the focal point of the whole network. Here is it clear that this router handles all intersegment traffic. Since the example assumes that the servers are all on separate segments from the users, essentially all application traffic except printing will pass through that router.
At the network layer the router is a single point of failure, just as the concentrator was at the physical layer. If either of these devices stops working, it will disable the entire network. This is why, in Figure 2-2, I replaced both the router and the concentrator.
I also made some other changes. I didn't duplicate the concentrators on the floors for the users, but I did duplicate the trunks connecting them to the basement. Why would I do this? Actually, there are a few good reasons for this. First, because I duplicated the backbone concentrators in the basement, I need to connect the floor concentrators to both of them. This way, if there is a failure of one of the backbone concentrators, it won't isolate an entire floor of users. This was the reasoning behind having a second connection to each of the servers.
Suppose there wasn't a backup interface on the servers, but the Core concentrators still duplicated as shown. If either of these concentrators then failed, the network would lose contact with all of the servers that were connected to that concentrator. Since all of this redundancy was implemented for these servers, it wouldn't do much good if they still had the same single point of failure. In the same way, the trunks between the Core and floor concentrators have been duplicated so that either Core concentrator could break without losing contact with the users. But the network could still lose contact with all of the users on that floor if the local concentrator failed. So why have I made just the trunks redundant and not the local concentrators?
The answer is that I'm not trying to make the network perfect, just better. There is a finite probability that any element anywhere in the network might fail. Before introducing redundancy, the network could lose connectivity to the entire floor if any of a long list of elements failed: the backbone concentrator, the floor concentrator, the fiber transceivers on either end of the trunk, the fiber itself. After the change, only a failure of the floor concentrator will bring down the whole floor. Section 2.2.7.1 will show some detailed calculations that prove this. But it is fairly intuitive that the fewer things that can fail, the fewer things that will fail.
Every failure has some cost associated with it, and every failure has some probability of occurring. These are the factors that must be balanced against the added expense required to protect against a failure. For example, it might be worthwhile to protect your network against an extremely rare failure mode if the consequences are sufficiently costly (or hazardous). It is also often worthwhile to spend more on redundancy than a single failure will cost, particularly if that failure mode occurs with relative frequency.
Conversely, it might be extremely expensive to protect against a common but inconsequential failure mode. This is the reasoning behind not bothering to back up the connections between end-user devices and their local hubs. Yes, these sorts of connections fail relatively frequently, but there are easy workarounds. And the alternatives tend to be prohibitively expensive.
The probability of a network device failing is so small that it usually isn't necessary to protect against multiple simultaneous failures. As I said earlier, most designers generally don't bother to back up a backup. Section 2.2.7.1 later in this chapter will talk more about this. But in some cases the network is so critically important that it contains several layers of redundancy.
A network to control the life-support system in a space station might fall into this category. Or, for more down-to-earth examples, a network for controlling and monitoring a nuclear reactor, or a critical patient care system in a hospital, or for certain military applications, would require extra attention to redundancy because a failure could kill people. In these cases the first step is to eliminate key single points of failure and then to start looking for multiple failure situations.
You'd be tempted to look at anything that can possibly break and make sure that it has a backup. In a network of any size or complexity, this will probably prove impossible. At some pragmatic level, the designer would have to say that any two or three or four devices could fail simultaneously.
This statement should be based on combining failure probabilities rather than guessing, though. What is the net gain in reliability by going to another level of redundancy? What is the net increase in cost? Answering these questions tells the designer if the additional redundancy is warranted.
When implementing redundancy, you should ask whether the additional complexity makes the network significantly harder to manage. Harder to manage usually has the unfortunate consequence of reducing reliability. So, at a certain point, it is quite likely that adding another level of redundancy could make the overall reliability worse.
In this example the network has been greatly improved at the cost of an extra concentrator and an extra router, plus some additional cards and fibers. This is the other key point to any discussion of redundancy. By its very definition, redundancy means having extra equipment and, therefore, extra expense. Ultimately, the cost must balance against benefit. The key is to use these techniques where they are needed most.
Returning to the reasons for not backing up the floor concentrator, the designer has to figure out how to put in a backup, how much this would cost, and what the benefit would be. In some cases they might put in a full duplicate system, as in the Core of the network in the example. This would require putting a second interface card into every workstation. Do these workstations support two network cards? How does failover work between them? With popular low-cost workstation technology, it is often not feasible to do this. Another option might be to just split the users between two concentrators. This way, the worst failure would only affect half the users on the biggest floor.
This wouldn't actually be considered redundancy, since a failure of either floor concentrator would still knock out a number of users completely. But it is an improvement if it reduces the probability of failure per person. It may also be an improvement if there is a congestion problem either within the concentrator or on the trunk to the Core.
Redundancy is clearly an important way of improving reliability in a network, particularly reliability against failures. But this redundancy has to go where it will count the most.
Redundancy may not resolve a congestion problem, for example. If congestion is the problem, sophisticated load-balancing schemes may be called for. This will be discussed in more detail in subsequent chapters.
But if fault tolerance is the issue, then redundancy is a good way to approach the solution. In general it is best to start at the Core (I will discuss the advantages to hierarchical network topologies later), where failures have the most severe consequences.
One of the keys to making redundancy work for fault-tolerance problems is the mechanism for switching to the backup. As a general rule, the faster and more transparent the transition, the better. The only exceptions are when an automatic switchover is not physically possible, or where security considerations outweigh fault-tolerance requirements.
The previous section talked about two levels of redundancy. There was a redundant router and a redundant concentrator. If the first Core concentrator failed, the floor concentrators would find the second one by means of the Spanning Tree protocol, which is described in some detail in Chapter 3. Different hardware vendors have different clever ways of implementing Spanning Tree, which I will talk more about later, but in general it is a quick and efficient way of switching off broken links in favor of working ones. If something fails (a Core concentrator or a trunk, for example), then the backup link is automatically turned on to try to restore the path.
Now, consider the redundancy involving the Core router. Somehow the backup router has to take over when the primary fails. There are generally two ways to handle this switchover. Either the backup router can "become" the primary somehow, or the end devices can make the switch. Since it is a router, it is addressed by means of an IP address (I am still talking about a pure TCP/IP network in this example, but the general principles are applicable to many other protocols).
So, if the end devices (the workstations and servers) are going to make the switch, then they must somehow decide to use the backup router's IP address instead of the primary router's IP address. Conversely, if the switch is to be handled by the routers, then the backup router has to somehow adopt the IP address of the primary.
The end stations may realize that the primary router is not available and change their internal routing tables to point to a second router. But in general this is not terribly reliable. Some types of end devices can update IP routing tables by taking part in a dynamic routing protocol such as Routing Information Protocol (RIP). This mechanism typically takes several minutes to complete.
Another way of dealing with this situation at the end device is to specify the default gateway as the device itself. This method is discussed in detail in Chapter 5. It counts on a mechanism called proxy ARP to deal with routing. In this case the second router would simply start responding to the requests that the first router previously handled.
There are many problems with this method. One of the worst is that it generally takes several minutes for an end station to remove the old ARP entries from its cache before trying the second router.
It is also possible to switch to the backup router manually by changing settings on the end devices. This is clearly a massive and laborious task that no organization would want to go through very often.
Each of these options is slow. Perhaps more importantly, different types of end devices implement these features differently. That's a nice way of saying that it won't work at all on some devices and it will be terribly slow on others. This leads to a general principle for automated fault recovery.
Wherever possible, the workings of the network should be hidden from the end device. There are many different types of end devices, all with varying levels of sophistication and complexity. It is not reasonable to expect some specialized, embedded system machine for data collection to have the same sophisticated capabilities as a high-end general-purpose server. Further, the network equipment is in a much better position to know what is actually happening in the network.
But the most important reason to let the network devices handle automated fault recovery is speed. The real goal is to improve reliability. And the goal of reliability is best served by hiding failures from the end devices. After all, the best kind of disaster is one that nobody notices. If the network can "heal" around the problem before anything times out and without losing any data, then to the applications and users it is as if it never happened.
When designing redundancy, automated fault recovery should be one of the primary considerations. Whatever redundancy a designer builds into the network, it should be capable of turning itself on automatically. So whenever considering redundancy, you should work with the fault-tolerance features of the equipment.
There are two main ways that automated fault-recovery systems can be implemented. I will generically refer to these as intrinsic and external. By intrinsic systems, I mean that the network equipment itself has software or hardware to make the transition to the backup mode. External, on the other hand, means that some other system must engage the alternate pathways or equipment.
An example of an external fault-recovery system would be a network-management system that polls a router every few seconds to see if it is available. Then, upon discovering a problem, it will run a script to reconfigure another router automatically to take over the functions of the first router. This example makes it clear that an automated external system is better than a manual process. But it would be much more reliable if the secondary router itself could automatically step in as a replacement.
There are several reasons why an intrinsic fault-tolerance system is preferable to an external one. First, it is not practical for a network-management system to poll a large number of devices with a high enough frequency to handle transitions without users noticing. Even if it is possible for one or two devices, it certainly isn't for more. In short, this type of scheme does not scale well.
Second, because the network-management box is most likely somewhere else in the network, it is extremely difficult for it to get a detailed picture of the problem quickly. Consequently, there is a relatively high risk of incorrectly diagnosing the problem and taking inappropriate action to repair it. For example, suppose the system is intended to reconfigure a backup router to have the same IP address as a primary router if the network-management system is unable to contact the primary. It is possible to lose contact with this router temporarily because of an unrelated problem in the network infrastructure between the management station and the router being monitored. Then the network-management system might step in and activate the backup while the primary is still present, thereby causing addressing conflicts in the network.
The third reason to caution against external fault-tolerance systems is that the external system itself may be unreliable. I mentioned earlier that the network must be more reliable than any device on it. If this high level of reliability is based on this lower requirement, it may not be helping much.
So it is best to have automatic and intrinsic fault-recovery systems. It is best if these systems are able to "heal" the network around faults transparently (that is, so that the users and applications don't ever know there was a problem). But these sound like rather theoretical ideas. Let's look briefly at some specific examples.
Consider the redundant router shown in Figure 2-2 and Figure 2-4. Suppose that one of the user workstations shown in the diagram is communicating with one of the servers. So packets from the workstation are intended for the IP address of the server. But at Layer 2 the destination address in these packets is the Ethernet MAC address of the primary router. This router is the default gateway for the VLAN. So it receives all packets with destination addresses not on the subnet associated with this VLAN, and it forwards them to the appropriate destination VLAN.
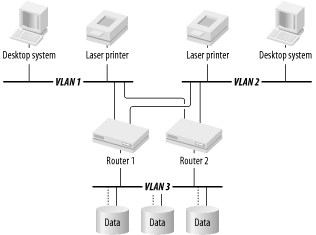
Now, suppose that this primary router's power supply has failed. Smoke is billowing out of the back, and it can no longer send or receive anything. It's gone. Meanwhile, the secondary router has been chattering back and forth with the primary, asking it whether it is working. It has been responding dutifully that it feels fine and is able to continue forwarding packets. But as soon as the power supply failed, it stopped responding to these queries. After a couple of repeated queries, the secondary router decides that it must step in to save the day. It suddenly adopts the Ethernet MAC address and the IP address of the primary on all of the ports that they have in common. Chapter 3 will discuss the details of how these high-availability protocols work.
The workstation has been trying to talk to the server while all of this is happening. It has sent packets, but it hasn't seen any responses. So it has resent them. Every one of these packets has a destination Ethernet MAC address pointing to the primary router and a destination IP address pointing to the server. For a few seconds while the secondary router confirmed that it was really appropriate to take over, these packets were simply lost. But most applications can handle the occasional lost packet without a problem. If they couldn't, then ordinary Ethernet collisions would be devastating.
As soon as the secondary router takes over, the workstation suddenly finds that everything is working again. It resends any lost packets, and the conversation picks up where it left off. To the users and the application, if the problem was noticed at all, it just looks like there was a brief slow-down.
The same picture is happening on the server side of this router, which has been trying to send packets to the workstation's IP address via the Ethernet MAC address of the router on its side. So, when the backup router took over, it had to adopt the primary router's addresses on all ports. When I pick up the discussion of these Layer 3 recovery mechanisms in Chapter 3, I talk about how to ensure that all of the router's functions on all of its ports are protected.
This is how I like my fault tolerance. As I show later in this chapter, every time a redundant system automatically and transparently takes over in case of a problem, it drastically improves the network's effective reliability. But if there aren't automatic failover mechanisms, then it really just improves the effective repair time. There may be significant advantages to doing this, but it is fairly clear that it is better to build a network that almost never appears to fail than it is to build one that fails but is easy to fix. The first is definitely more reliable.
There is another type of automatic fault tolerance in which the backup equipment is active during normal operation. If the primary and backup are set up for dynamic load sharing, then usually they will both pass traffic. So most of the time the effective throughput is almost twice what it would be in the nonredundant design. It is never exactly twice as good because there is always some inefficiency or lost capacity due to the load-sharing mechanisms. But if it is implemented effectively, the net throughput is significantly better.
In this sort of load-balancing fault-tolerance setup, there is no real primary and backup system. Both are primary, and both are backup. So either can fail, and the other will just take up the slack. When this happens, there is an effective drop in network capacity. Users and applications may notice this change as slower response time. So when working with this model, one generally ensures that either path alone has sufficient capacity to support the entire load.
The principal advantage to implementing fault tolerance by means of load balancing is that it provides excess capacity during normal operation. But another less obvious advantage is that by having the backup equipment active at all times, one avoids the embarrassing situation of discovering a faulty backup only during a failure of the primary system. A hot backup system could fail just as easily as the primary system. It is possible to have a backup fail without being noticed because it is not in use. Then if the primary system fails, there is no backup. In fact, this is worse than having no backup because it has the illusion of reliability, creating false confidence.
One final advantage is that the money spent on extra capacity results in tangible benefits even during normal operation. This can help with the task of securing money for network infrastructure. It is much easier to convince people of the value of an investment if they can see a real improvement day to day. Arguments based on reducing probability of failure can seem a little academic and, consequently, a little less persuasive than showing improved performance.
So dynamic load-balancing fault tolerance is generally preferable where it is practical. But it is not always practical. Remember the highway example. Suppose there are two bridges over a river and a clever set of access roads so that both bridges are used equally. In normal operation, this is an ideal setup. But now suppose that one of these bridges is damaged by bad weather. If half of the cars are still trying to use this bridge and one-by-one are plunging into the water, then there is a rather serious problem.
This sounds silly with cars and roads, but it happens regularly with networks. If the load-balancing mechanism is not sensitive to the failure, then the network can wind up dropping every other packet. The result to the applications is slow and unreliable performance. It is generally worse than an outright failure because, in that case, people would give up on the applications and focus on fixing the broken component. But if every other packet is getting lost, it may be difficult to isolate the problem. At least when it breaks outright, you know what you have.
More than that, implementing the secondary system has doubled the number of components that can each cause a network failure. This directly reduces the reliability of the network because it necessarily increases the probability of failure.
Further, if this setup was believed to improve reliability, then it has provided an illusion of safety and a false sense of confidence in the architecture. These are dangerous misconceptions.
So, where dynamic load balancing for fault tolerance is not practical, it is better to have a system that automatically switches to backup when a set of clearly defined symptoms are observed. Preferably, this decision to switch to backup is made intrinsically by the equipment itself rather than by any external systems or processes.
If this sort of system is employed as a fault-tolerance mechanism, it is important to monitor the utilization. It is common for network traffic to grow over time. So if a backup trunk is carrying some of the production load, it is possible to reach a point where it can no longer support the entire load in a failure situation. In this case the gradual buildup of traffic means that the system reaches a point where it is no longer redundant.
If this occurs, traffic will usually still flow during a failure, but there will be severe congestion on these links. This will generally result in degraded performance throughout the network.
It is universally true that automatic recovery processes are better than manual processes. There is far too much uncertainty in manual procedures. Differences in levels of experience and expertise in the network-operations staff can mean that sometimes the manual procedures work brilliantly. Sometimes the same procedure can fail catastrophically because of incorrect problem determination or execution. Almost invariably, human-rooted procedures take longer both to start and to complete than automatic processes.
There are only two valid reasons to use a manual recovery process. Either there is no cost-effective way to implement a reliable automatic system, or there are significant security concerns with an automatic system.
In the first case, it is generally wise to re-evaluate the larger design to understand why automatic features of the equipment are not applicable or are too expensive. Redesigning other elements could allow application of automatic fault recovery. But presence of key pieces of older equipment might also make automation impossible. In this case it would be wise to look at upgrading to more modern network technology.
The security reasons for manual processes are more difficult to discuss. But they come down to manually ensuring that the system taking over the primary function is legitimate. For example, a concern might be that an imposter device will attempt to assert itself as a new primary router, redirecting sensitive data for espionage reasons. Or a dial backup type system might be unwilling to accept connections from remote sites unless they are manually authenticated, thus ensuring that this backup is not used to gain unauthorized access to the network.
Usually there are encryption and authentication schemes associated with these sorts of automated processes to protect against exactly these concerns. In some cases the data is considered too sensitive to trust with these built-in security precautions. So, in these cases a business decision has to be made about which is more important, reliability or security.
One often hears the term single point of failure tossed around. In a network of any size or complexity, it would be extremely unusual to find a single device that, if it failed, would break the entire network. But it is not unusual to find devices that control large parts of the network. A Core router will handle a great deal of intersegment traffic. Similarly, a switch or concentrator may support many devices. So, when I talk about single points of failure, I mean any network element that, if it failed, would have consequences affecting several things. Further, for there to be a single point of failure, there must be no backup system. If a single point of failure breaks, it takes out communication with a section of the network.
Clearly single points of failure are one of the keys to network stability. It is not the only one, and too much effort spent on eliminating single points of failure can lead to levels of complexity that also cause instability. So it is important to be careful with this sort of analysis. It can't be the only consideration.
I discuss other factors contributing to stability later, but for now I want to focus on this one. What makes one single point of failure more severe than another depends on the network. It will depend on how many users are affected, what applications are affected, and how important those users and applications are to the organization at that specific point in history. Losing contact with an application that is only used one day per year doesn't matter much unless it happens on that one day. While it's certainly not true that everybody in an organization is of equal value to the organization (or they'd all make the same amount of money), the number of people affected by a failure is clearly an important factor.
In general it isn't possible to say definitively which failure points are the most important. And it isn't always practical to eliminate them all. In Figure 2-2, two single points of failure at the Core of the network were eliminated by adding redundant equipment. But the concentrators on each floor were not made redundant. If one of these concentrators fails, the network will still lose connection to all of the users on that floor.
The simplest way to qualitatively analyze stability is to draw out a complete picture of the network and look at every network device one by one. In the previous section, both the physical- and network-layer diagrams were necessary to see all of the key points in the network, and the same is true here. In the preceding simple example, the router's critical function in the network was not immediately obvious from the physical-layer diagram. In a more complicated network the dependencies could be even less clear.
Look at each box in both of your drawings and ask what happens if this device fails. You may want to look at both drawings at the same time, referring back and forth between them. If the answer is that another device takes over for it, then you can forget about this device for the time being and move on to the next device. Similarly, if the device you are looking at exists purely as a standby, then you can skip it. What remains at the end are all of the places where something can go seriously wrong. In the process, remember to include the connections themselves. Fiber optic cable can go "cloudy," and any cable can be accidentally cut. Consider, for example, what would happen if somebody accidentally cut through an entire fiber conduit. It happens. Many network designers make a point of running their redundant connections through separate conduits.
For each of the remaining elements, it is useful to ask qualitatively how serious a problem it is if it fails. What is affected? How many users are unable to do their jobs? In many cases you will find that some people are unable to run some applications. How important is this to the organization? Rate these problem spots.
Doing this, it should quickly become apparent where the most glaring trouble spots are in your network. In effect you are doing the calculations of the next section "by eye." This tends to assume that the Mean Time Between Failure (MTBF) values for all network elements are similar. That may not be accurate if you are comparing a small workgroup hub to a large backbone switch. But, at the same time, chances are that the backbone switch is a much more critical device, in that it probably supports more traffic and more users.
As was shown in the previous section, the more of these key failure zones that can be eliminated, the better the overall stability of the network.
Consider an example network. Figure 2-5 and Figure 2-6 show the Layer 1/2 and Layer 3/4 views of the same fictitious network. There are many problems with this network, making it a good example for analysis. But clearly there has been some effort at improving the stability. The engineers who run this imaginary network have twinned the switches carrying the router-to-router VLANs, "Core A" and "Core B." And they have built all of the user VLANs, the server VLAN, and the WAN with redundant connections as well. But there are still several serious problems.
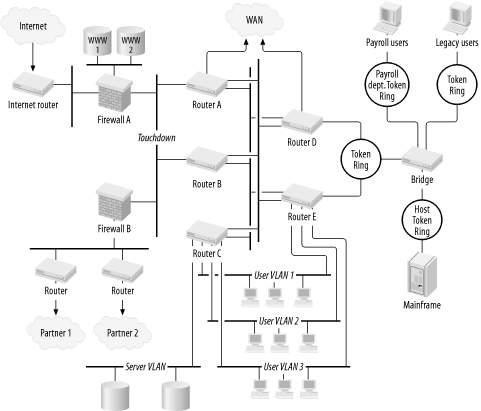
Look at the "touchdown"[2] Ethernet segment in Figure 2-6. Clearly there is a single point of failure in each of the two firewalls. But perhaps this company's Internet usage and the connections to its partner firms are considered of lower importance to other Core parts of the network. So this may be all right. But they have made an effort to make the connections to the touchdown segment redundant, attaching it to both Router A and Router B.
[2] This is a relatively common technique for connecting external networks into a LAN. It will be covered in more detail in Chapter 3.
Look at the same part of the network in Figure 2-5. The touchdown segment is carried entirely on one Ethernet hub. So the probability of failure for their Internet access, for example, is actually higher than the probability of failure for the firewall.
At the Core of the network, care has been taken to include two main switches, Core switch A and Core switch B. But then both of the main application servers were connected to switch B. This means that much of the advantage of redundancy has been lost.
Now skip over to the right-hand sides of these diagrams. Figure 2-6 shows that the bridge that interconnects all of the Token Rings is a single point of failure. But there are two connections for Routers D and E. Now look at Figure 2-5.
Making two router connections seems to have been an almost wasted effort. After leaving the routers, all the traffic passes through a single Token Ring MAU, through a single fiber transceiver, through a single pair of fiber strands, through another single fiber transceiver, and then to a single bridge. These are all single points of failure. Connecting several single points of failure together in serial allows the failure of any one device to break the entire chain. So clearly the probability of failure is significantly higher than it has to be.
If you are dealing with a high-availability application where certain outages would be serious disasters, then the process of finding danger spots becomes more difficult. In these cases, it is best to break down the network into zones and deal with them separately. I discuss how to build network zones in the discussion of topology in Chapter 3. This concept makes isolating your problems much easier. The idea is to have a few well-controlled points where one network zone touches the next one. Then, as long as there is fault tolerance in the interconnections, you can analyze the zones more or less in isolation.
To deal with multiple failure situations, you can follow a strategy similar to the one described in the previous case, which was looking only for single points of failure. Except that this time it will be necessary to make several passes through. On the first pass, you will look at every network element and decide what will happen if it fails. In a high-availability network, the answer to each of these questions should be that there is a redundant system to take over for the failed element automatically.
Next you will systematically look at each device and assume that it has already failed. Then go through the remainder of the network and analyze what would happen for each element if it failed in the absence of that first failed element. This process sounds time consuming, but it is not quite as bad as it sounds.
Suppose there are 100 elements to consider in this zone. Remember to include all connections as elements that can fail as well, so the number will usually be fairly high. The initial analysis has already established that any one element can fail in isolation without breaking the network. Now start by looking at element number 1, and supposing it has failed, decide what happens if element number 2 fails. And continue this process through to element 100. On the next pass you start by assuming that element number 2 has failed. This time you don't need to consider what happens if element number 1 fails, because you did that in the last pass. So each pass through the list is one shorter than the last one.
In practice, this sort of qualitative analysis usually takes many hours to complete. But it is a worthwhile exercise, as it will uncover many hidden problems if done carefully. Most of the time it will be obvious that there is no problem with the second element failing, since it is backed up by another element unrelated to the first failure. In fact, it is often worth doing this exercise in a less mission-critical network because it will show how vulnerabilities are connected.
But, as I mentioned earlier in passing, just eliminating the single points of failure does not guarantee a stable network. The sheer complexity of the result can itself be a source of instability for several reasons. First and most important, the more complex the network is, the greater the chance that a human will misunderstand it and inadvertently break it. But also, the more complex a network, the more paths there will be to get from point A to point B. As a result, the automated fault-recovery systems and automated routing systems will have a considerably harder time in finding the best path. Consequently, they will tend to take much longer in converging and may try to recalculate the paths through the network repeatedly. The result is a frustratingly slow and unreliable network despite the absence of single points of failure.
I have talked about implementing redundancy where it is most needed. But so far I have only given general comments about where that might be. I've mentioned duplicating systems "in the Core" and at "single points of failure," but the methods have been mostly qualitative and approximate. As a network designer, you need to know where to look for problems and where to spend money on solutions. This requires more rigorous techniques.
There is an analytical technique based on MTBF that provides a relatively precise way of numerically estimating probabilities of failure for not only individual components in a network, but also for whole sections of networks. I will demonstrate this technique. I will also discuss some more qualitative methods for finding potential problem spots.
One of the most important numbers your equipment manufacturer quotes in the specification sheet is the Mean Time Between Failures (MTBF). But this value is frequently misunderstood and misused. So I will discuss the concept a little bit before going on.
This number just represents a statistical likelihood. It means that half (because it's a statistical "mean") of all equipment of this type will no longer be functioning after this length of time. It does not mean that sudden and catastrophic failure will occur at the stroke of midnight. Failure can happen at any time. But just giving an average without saying anything about the shape of the curve makes it difficult to work with.
Figure 2-7 shows some possible versions of what the curve might look like. These curves plot the number of device failures as a function of time. There are N total devices, so at time MTBF, there are N/2 devices remaining.
The thick solid line represents a very ideal world where almost all of the gear survives right up until moments before the MTBF. Of course, the price for this is that a large number of devices then all fail at the same time.
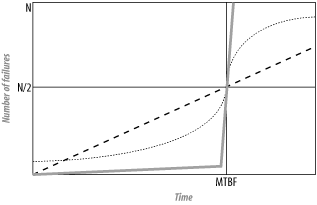
The dashed line, on the other hand, shows a sort of worst-case curve, in which the same number of devices fail every day. This is probably not a realistic approximation either because there are a lot of devices that either don't work when you open the box or fail soon after. Then age will take a toll later as gear gradually burns out through heavy use. The dotted curve represents a more realistic curve.
But the interesting thing is that, when you look at these curves, it's clear that the dashed line isn't such a bad approximation after all. It's going to be close. And up until the MTBF time, it will tend to overestimate the probability of failure. It's always a good idea to overestimate when it comes to probability of failure, because the worst you can do is end up with an unusually stable and reliable network. It's also going to be the easiest to do calculations with.
So the dashed line is the one I use for finding the most common failure modes. The slope of this line gives the failure rate, the number of failures per unit time, and because it is a straight line, the approximation assumes a constant failure rate. A little arithmetic shows that the line rises by N/2 in a distance of MTBF, so the slope is N/(2 x MTBF). So, if the MTBF is 10 years, then you will expect to see 5% of your devices fail every year, on average. If the MTBF is 20 years, then the value drops to 2.5%. Most network-equipment manufacturers quote an MTBF in this range.
If you had only one device, then a 5% per year failure rate is probably quite acceptable. You may not care about redundancy. But this book is concerned with large-scale networks, networks with hundreds or thousands of devices. At 5% per year, out of a network of 1000 devices, you will expect to see 50 failures per year. That's almost one per week.
The important point to draw from this is that the more devices you have, the greater the chances are that one of them will fail. So, the more single points of failure in the network, the greater the probability of a catastrophic failure.
So the MTBF gives, in effect, a probability of failure per unit time. To find the probability for simultaneous failures, you need a way of combining these probabilities. I have already described the method of simply adding probabilities to find the aggregate failure rate. But this is a different problem. The important question here is the probability of exactly two or three or four simultaneous failures.
The naïve approach to combining probabilities would be to say that the probability of two simultaneous failures is twice the probability of one. This would be close to true for very small values, but not quite right. To see this, imagine a coin toss experiment. The probability of heads is 50%. The probability of flipping the coin 3 times and getting 2 heads is not 100%. And it certainly isn't equal to the probability of flipping the coin 100 times and getting 2 heads.
Now suppose that it is an unfair coin that has a probability P of coming up heads. In fact, it's an extremely unfair coin. P is going to be less than 1%. Later I adapt this simple probability to be a probability of failure per unit time, as it is needed for combining these MTBF values. But first I need the probability, kPn, of tossing the coin n times and getting heads k times. The derivation of this formula is shown in Appendix A.
![]()
For network MTBF, the interesting values are related to number of failures per unit time. If the MTBF value is M, then you can expect N/(2 x M) failures out of a set of N per unit time. If N = 1, then this is the probability per unit time of a particular unit failing. But you can't just plug this into the formula for kPn. Why not? Look at the formula. It contains a factor that looks like (1-P)n-k. The number 1 has no units. So the number P can't have units either, or the formula is adding apples to oranges.
So it is necessary to convert this probability per unit time to a net probability. The easiest way to do this is to decide on a relevant time unit and just multiply it. This time unit shouldn't be too short or too long. The probability of having two failures in the same microsecond is very small indeed. And the probability of having two failures in the same year is going to be relatively large, but it is quite likely that the first problem has been fixed before the second one occurs.
This is the key to finding the right length of time. How long does it take, on average, to fix the problem? Note that this is not the length of time for the backup to kick in, because the result is going to show how appropriate that backup is. If the backup fails before the primary unit has been fixed, then that's still a multiple-failure situation. So the best unit is the length of time required to fix the primary fault.
For this I like to use one day. Sometimes it takes longer than one day to fix a major problem; sometimes a problem can be fixed in a few hours. But a one-day period is reasonable because, in most networks, a day with more than one major-device failure is an exceedingly busy day. And when there are multiple device failures in one day, there is usually a lot of reporting to senior management required. In any case, it generally takes several hours to repair or replace a failed device, so a one-day period for the time unit seems appropriate. At worst, it will overestimate the failure rates slightly, and it's always better to overestimate.
I will denote thie MTBF per-day value by the letter M. So the probability of one particular device failing in a given day is P = 1/2M.
So, substituting into the probability formula gives:
![]()
where m = M/1 day.
This formula gives the probability that, in a network of n devices, each with an MTBF value of M, there will be k failures in one day. Figure 2-8 is a graph of the probabilities for some representative values. Notice that for most of the values plotted, it is quite rare to have any failures at all. But for a network of 1000 nodes, each with a 100,000-hour MTBF, there will be failures on about 1 day in 10. If that same network had 10,000 nodes in it, the analysis predicts that only 30% of all days will have no failures. 36% of days would have some device fail, and about 1 day in 5 would see 2 or more failures. Even the smaller network with only 1000 nodes would have days with 2 failures 0.6% of the time. That amounts to just over 2 days per year. So it will happen.
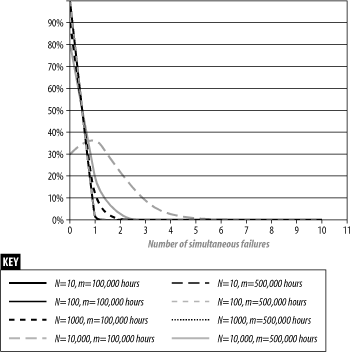
Generally you want to work out these probabilities for your whole network. You should plan your network for a level of redundancy that the business can handle. Personally, I don't like to deal with multiple failures in a single day, so I plan my networks so that these bad days are expected much less than once every year. But you need to determine what your business and your network-management team can handle.
In general, in a multivendor network, there will be many different MTBF values. In fact, many vendors quote distinct MTBF values for every component of a modular device. They do this because how you combine these values to find the number relevant to your network depends greatly on how you decide to use the device.
This section will describe how to combine the values. I start by looking at how to combine the MTBF values for a single device and then move on to how to combine these values for various elements making up a network. A common technique for this sort of estimation says that the chain is as strong as its weakest link. But this is not actually a very good rule, as can be seen with a simple example.
Suppose you have a generic device. Maybe it's a router. Maybe it's a switch of some sort. It doesn't really matter for this example. Table 2-1 shows some fairly typical made-up values for the MTBFs of these various components.
|
Component |
Hours |
|---|---|
|
Chassis |
2,000,000 |
|
Power supply |
100,000 |
|
Processor |
200,000 |
|
Network card |
150,000 |
It is extremely rare for the chassis to fail. If it does fail, it is usually due to damage such as bent pins from swapping cards too aggressively or heat damage to the backplane. Power supplies, however, are much less reliable. Typically the power supply is the most likely component failure in any piece of electronic equipment. See Table 2-2 for failure probabilities of typical components.
|
Component |
Probability |
|---|---|
|
Chassis |
0.0006% |
|
Power supply |
0.0120% |
|
Processor |
0.0060% |
|
Network card |
0.0080% |
So, this generic device has a chassis, two power supplies (for redundancy), a processor module, and two network modules. There is no redundancy for the processor or for the network modules. What is the aggregate MTBF for the device? This could involve any failure to any component. But the twist is that, if one of the power supplies fails, the other will take over for it.
First these MTBF values have to be converted to probabilities of failure per day. Recall that the formula for this is just 1/(2m), where m = MTBF/1 day.
First combine the probabilities for the two power supplies failing simultaneously. That would be two simultaneous failures out of a set of two. This is just 2P2 = P2 in the joint probability formula. The square of 0.0120% is a very small number, 1.44 x 10-6%. So clearly the decision to use redundant power supplies has significantly improved the weakest link in this system.
Any of the remaining components can fail independently and count as a device failure, so you can just add these probabilities to get the net probability.
![]()
You can now convert this back to an aggregate MTBF for the device. Since P = 1/(2m), m = 1/(2P). So, in this case, m = 53,100 hours.
As you can see, the weakest-link rule is quite wrong. It would have said that you could neglect the power supplies because they are redundant (and it would have been right in saying that). Then it would have picked out the network card's 150,000-hour MTBF value.
The trouble with this is that it completely neglects the fact that there are several elements here, any of which can fail. The chances of getting into a car accident are exceedingly small. Most people only have a few in their entire lives. And yet, in a large city there are accidents every day. It's the same with networks. The more components you have, the more likely something will fail.
To take this example slightly further, let's try to understand why many hardware vendors offer the capability of redundant processor modules. In this case the net probability is:
![]()
which corresponds to an aggregate MTBF for the device of 72,300 hours. So, duplicating the processor module has improved the net MTBF for the device by 36%.
There is one final example to look at before moving on to calculating MTBF values for an entire network. Often, particularly for power supplies, devices employ what is called "N+1" redundancy. This means that there is one extra power supply in the box. Suppose the device needs only 3 power supplies to work. Then you might install a fourth power supply for redundancy. For a complete failure, you need to lose 2 of the 4 power supplies. To calculate the probability for this, use the formula derived in the previous section:
![]()
with k = 2 and n = 4.
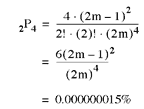
Recall that the single power-supply failure probability was 0.0120%. For two fully redundant power supplies the probability is (0.0120%)2 = 0.00000144%. So it becomes clear that N+1 redundancy in these small numbers provides a large benefit and is a cost-effective strategy.
The net probability of failure for the entire device (with dual processors, as in the previous example) would become:
![]()
which is effectively the same as the previous example with full redundancy for the power supplies.
As a quick aside, consider how N+1 redundancy works for larger values of N. How much can the situation be improved by adding one extra hot standby? In other words, I want to compare the probability for one failure out of N with the probability for two simultaneous failures:
![]()
and:
![]()
So 2Pn / 1Pn ~ n/4m. This means that as long as N is much smaller than 4 times the MTBF in days, the approximation should be reasonable. But, for example, if the MTBF were 100 days, then it would be a very bad idea to use N+1 redundancy for 25 components. In fact, it would probably be wise to look at N+2 or better redundancy long before this point.
The same prescription can be used for calculating the probability of failure for an entire network. Consider the network shown in Figure 2-1 and Figure 2-2. How much has the network's net MTBF improved by making the Core redundant? Note, however, that there are failures in this more general case that do not wipe out the entire network. For example, if any of the floor concentrators fails, it will affect only the users on that floor. However, it is still useful to do this sort of calculation because it gives an impression of how useful it has been to add the redundancy.
Calculating the MTBF for only the Core could well miss the possibility that the worst problems do not lie in the Core. In any case, it is worthwhile understanding how often to expect problems in the entire network.
Table 2-3 presents some representative fiction about the MTBF values for the individual components in the network. Note that I have included the fiber runs between the floors, but I assume that the fiber transceivers are built into the concentrators, and are included in the MTBF for the device. Also note that for simplicity, I use the same model of device for the floor and Core concentrators. This would probably not be true in general.
|
Component |
Hours |
Probability |
|---|---|---|
|
Concentrator |
150,000 |
0.0080% |
|
Fiber connection |
1,000,000 |
0.0012% |
|
Router |
200,000 |
0.0060% |
Adding up the net probability for the network without redundancy gives:
![]()
So the net MTBF is 28,846 hours. And, with redundancy:
![]()
which gives a net MTBF of 38,460 hours. This is a 33% improvement in MTBF, or a 25% improvement in Pnet. So implementing redundancy has helped significantly. Looking specifically at the terms, one can easily see that the terms for the Core are now very small. The bulk of the failures are expected to occur on the floor concentrators now. Interestingly, this was true even before introducing the Core redundancy. But, clearly, the redundancy in the Core has radically improved things overall.
This way of looking at reliability provides another particularly useful tool: it shows where to focus efforts in order to improve overall network reliability further.
It could be that there are only 3 users on the first floor and 50 on the second. In some sense, the failure of the second floor is more important. So it may be useful to produce a weighted failure rate per user. To do this, look at each device and how many users are affected if it fails. Then, in the calculation of Pnet, multiply the number of users by the probability. When you do this, the number is no longer a probability, and you can no longer convert it back to an MTBF. You can only use it as a relative tool for evaluating how useful the change you propose to make will be. See Table 2-4 for user failure probabilities for sample components.
|
Component |
Hours |
Probability |
Users |
|---|---|---|---|
|
First floor concentrator |
150,000 |
0.0080% |
3 |
|
First floor fiber connection |
1,000,000 |
0.0012% |
3 |
|
Second floor concentrator |
150,000 |
0.0080% |
50 |
|
Fiber connection |
1,000,000 |
0.0012% |
50 |
|
Third floor concentrator |
150,000 |
0.0080% |
17 |
|
Third floor fiber connection |
1,000,000 |
0.0012% |
17 |
|
Backbone concentrator |
150,000 |
0.0080% |
70 |
|
Router |
200,000 |
0.0060% |
70 |
So adding up the weighted probability for the nonredundant case gives:
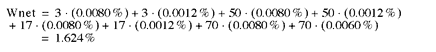
I have changed the symbol from Pnet to Wnet. This is to remind you that this is not a real probability anymore. It is just a tool for comparison.
Now let's look at the redundant case:
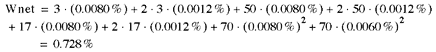
This shows that the changes have improved the per-user reliability by better than a factor of 2. It also shows that doing any better than this will mean doing something for the people on the second floor, because the terms corresponding to them make up more than 2/3 of the total value of Wnet.
But perhaps network engineering is on the first floor and marketing or bond trading is on the second. In this case, losing the 50 users on the second floor could be a net benefit to the company, but losing the 3 network engineers would be a disaster. If this is the case, you may want to use another weighting scheme, based on the relative importance of the users affected. Remember, though, that these weighted values are no longer probabilities. Weighting the different terms destroys what mathematicians call normalization. This means that these W values will not sum to 1. So you can't use the numbers where you would use probabilities, for example, in calculating MTBF.