Page 23           Mathematics             Mathematics is the science of relationships between numbers, between spatial configurations, and abstract structures. The main divisions of pure mathematics include arithmetic, algebra, geometry, trigonometry, and calculus. Mechanics, statistics, numerical analysis, computing, the mathematical theories of astronomy, electricity, optics, thermodynamics, and atomic studies come under the heading of applied mathematics.             During the 20th century mathematics became diversified. Each specialist subject is being studied in far greater depth and advanced work in some fields may be unintelligible to researchers in other fields. Mathematicians working in universities have had the economic freedom to pursue the subject for its own sake. Nevertheless, new branches of mathematics have been developed which are of great practical importance and which have basic ideas simple enough to be taught in schools. Probably the most important of these is the mathematical theory of statistics in which much pioneering work was done by the English mathematician Karl Pearson. Another new development is operations research, which is concerned with finding optimum courses of action in practical situations, particularly in economics and management. Higher mathematics has a powerful tool in the high-speed electronic computer, which can create and manipulate mathematical "models" of various systems in science, technology, and commerce.             Traditionally the subject of mathematics is divided into arithmetic, which studies numbers; algebra, which studies structures; geometry, which studies space; analysis, which studies infinite processes (in particular, calculus); and probability theory and statistics, which study random processes. Modern additions to school syllabuses such as sets, group theory, matrices, and graph theory are sometimes referred to as "new" or "modern" mathematics.             Numbers             number systems             Numbers are symbols used in counting or measuring. Our everyday number system is the decimal ("proceeding by tens") system. The ancient Egyptians, Greeks, Romans, and Babylonians all evolved number systems, although none had a zero, which was introduced from India by way of Arab mathematicians in about the 8th century A.D. and allowed a place-value system to be devised on which the decimal system is based. Other systems are mainly used in computing and include the binary number system, octal number system, and hexadecimal number system.             what is a base? A base is the number of different single-digit symbols used in a particular number system. In our usual (decimal) counting system of numbers (with symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, 9) the base is 10. In the binary number system (see below), which has only the symbols 1 and 0, the base is two.             A base is also a number that, when raised to a particular power (that is, when multiplied by itself a particular number of times as in 102 = 10 × 10 = 100), has a logarithm (see below) equal to the power. For example, the logarithm of 100 to the base ten is 2.             In general, any number system subscribing to a place-value system with base value b may be represented by . . . b4, b3, b2, b1, b0, b–1, b–2, b–3, . . .

 

 

Page 24 Number Systems       Binary (Base 2)     Octal (Base 8) Decimal (Base 10) Hexadecimal (Base 16) 0 0 0 0 1 1 1 1 10 2 2 2 11 3 3 3 100 4 4 4 101 5 5 5 110 6 6 6 111 7 7 7 1000 10 8 8 1001 11 9 9 1010 12 10 A 1011 13 11 B 1100 14 12 C 1101 15 13 D 1110 16 14 E 1111 17 15 F 10000 20 16 10 11111111 377 255 FF 11111010001 3721 2001 7D1           Hence in base ten the columns represent . . . 104, 103, 102, 101, 100, 10–1, 10–2, 10–3 . . . , in base two . . . 24, 23, 22, 21, 20, 2–1, 2–2, 2–3 . . ., and in base eight . . . 84, 83, 82, 81, 80, 8–1, 8–2, 8–3. . . . For bases beyond 10, the denary numbers 10, 11, 12, and so on must be replaced by a single digit. Thus in base 16, all numbers up to 15 must be represented by single-digit "numbers," since 10 in hexadecimal would mean 16 in decimal. Hence decimal 10, 11, 12, 13, 14, 15 are represented in hexadecimal by letters A, B, C, D, E, F.             Other number systems use other bases. For example, numbers to base two (binary numbers), using only 0 and 1, are commonly used in digital computers to represent the two-state "on" or "off" pulses of electricity. The Babylonians, however, used a complex base-sixty system, residues of which are found today in the number of minutes in each hour and in angular measurement (6 × 60 degrees). The Mayas used a basetwenty system.       Babylonian and Egyptian Mathematics http://www.history.mcs.st-and.ac.uk/~history/HistTopics/Babylonian_and_Egyptian.html         Description of the mathematics of these two early civilizations. The site includes maps of the area at the time, images of tablets and scrolls dating back to that era, and also a list of publications for further reference.           Roman numerals             Roman numerals are an ancient European number system using symbols different from Arabic numerals (the ordinary numbers 1, 2, 3, 4, 5, and so on). The seven key symbols in Roman numerals, as represented today, are I (1), V (5), X (10), L (50), C (100), D (500), and M (1,000). There is no zero, and therefore no place-value as is fundamental to the Arabic system. The first ten Roman numerals are I, II, III, IV (or IIII), V, VI, VII, VIII, IX, and X. When a Roman symbol is preceded by a symbol of equal or greater value, the values of the symbols are added (XVI = 16).             When a symbol is preceded by a symbol of less value, the values are subtracted (XL = 40). A horizontal bar over a symbol indicates a multiple of 1,000 (= 10,000). Although addition and subtraction are fairly straightforward using Roman numerals, the absence of a zero makes other arithmetic calculations (such as multiplication) clumsy and difficult.     Roman Arabic Roman Arabic I 1 II 2 III 3 IV 4 V 5 VI 6 VII 7 VIII 8 IX 9 X 10 XI 11 XIX 19 XX 20 XXX 30 XL 40 L 50 LX 60 XC 90 C 100 CC 200 CD 400 D 500 CM 900 M 1,000           decimal number system             The decimal numeral system, or denary number system, evolved from the Hindu-Arabic number system and is the most commonly used number system today. It

 

 

Page 25         employs ten numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and is said to operate in "base ten." In a base-ten number, each position has a value ten times that of the position to its immediate right; for example, in the number 23 the numeral 3 represents three units (ones), and the numeral 2 represents two tens. Decimal numbers do not necessarily contain a decimal point; 563, 5.63, and –563 are all decimal numbers.             Decimal numbers may be thought of as written under column headings based on the number ten. For example, the number 2,567 stands for 2 thousands, 5 hundreds, 6 tens, and 7 ones. Large decimal numbers may also be expressed in floating-point notation.       History of Numbers http://www.islam.org/Mosque/ihame/Ref6.htm         Account of how numbers developed from their ancient Indian origins to the Modern Arabic numerals that are generally used today. There is a brief description of numbering systems used by the ancient Egyptians, Greeks, and Romans, and some of the problems these systems presented.           binary number system Binary numbers were first developed by the German mathematician Gottfried Leibniz in the late 17th century. The binary system is a system of numbers to base two, using combinations of the digits 1 and 0.             The value of any position in a binary number increases by powers of 2 (doubles) with each move from right to left (1, 2, 4, 8, 16, and so on). For example, 1011 in the binary number system represents (1 × 8) + (0 × 4) + (1 × 2) + (1 × 1), which adds up to 11 in the decimal system.             The value of any position in a normal decimal, or base-ten, number increases by powers of 10 with each move from right to left (1, 10, 100, 1,000, 10,000, and so on). For example, the decimal number 2,567 stands for:             (2 × 1,000) + (5 × 100) + (6 × 10) + (7 × 1)             Codes based on binary numbers are used to represent instructions and data in all modern digital computers, the values of the binary digits (contracted to "bits") being stored or transmitted as, for example, open/closed switches, magnetized/unmagnetized disks and tapes, and high/low voltages in circuits. Because the main operations of subtraction, multiplication, and division can be reduced mathematically to addition, digital computers carry out calculations by adding, usually in binary numbers in which the numerals 0 and 1 can be represented by off and on pulses of electric current.             types of numbers             Numbers can be categorized broadly as real and complex. Concepts such as negative numbers, rational numbers, and irrational numbers can be rigorously and precisely defined in terms of the natural numbers. There remains then the problem of defining the natural numbers. A modern approach defines the natural numbers in terms of sets (see below). Zero is defined to be the empty set: 0 = ø (i.e. the set with no elements). Then 1 is defined to be the union of 0 and the set that consists of 0 (which is a set with 1 element, zero). Now we can define 2 as the union of 1 and the set containing 1 (which is a set containing 2 elements, zero and one), and so on.             An alternative procedure for constructing a number system is to define the real numbers in terms of their algebraic and analytical properties.             binary number system The capital letter A represented in binary form.             real numbers Real numbers include all rational numbers (integers, or whole numbers, and fractions) and irrational numbers (those not expressible as fractions). Rational numbers are whole numbers, or integers, and fractions. The whole numbers are represented by the natural numbers, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, which give a counting system that, in the decimal system, continues 10, 11, 12, 13, and so on. Fractions of these numbers are represented as, for example, 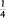, , , 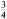or as decimal fractions (0.25, 0.5, 0.75).             Irrational numbers cannot be represented in this way and require symbols, such as Ö2, p, and e. They can be expressed numerically only as the (inexact) approximations 1.414, 3.142, and 2.718 (to three places of decimals) respectively. The symbols p and e are also examples of transcendental numbers, because they (unlike Ö2) cannot be derived by solving a polynomial equation (an equation with one variable quantity) with rational coefficients (multiplying factors).             complex numbers Complex numbers include the real numbers described above and imaginary numbers,

 

 

Page 26         complex number A complex number can be represented graphically as a line whose end- point coordinates equal the real and imaginary parts of the complex number. This type of diagram is called an Argand diagram after the French mathematician Jean Argand (1768–1822) who devised it.             which are real-number multiples of the square root of –1. A complex number is a number written in the form a + ib, where a and b are real numbers and i is the square root of –1 (that is, i2 = –1); i used to be known as the "imaginary" part of the complex number. Some equations in algebra, such as those of the form             cannot be solved without recourse to complex numbers, because the real numbers do not include square roots of negative numbers.             The sum of two or more complex numbers is obtained by adding separately their real and imaginary parts, for example:             Complex numbers can be represented graphically on an Argand diagram, which uses rectangular Cartesian coordinates in which the x-axis represents the real part of the number and the y-axis the imaginary part. Thus the number z = a + bi is plotted as the point (a, b). Complex numbers have applications in various areas of science, such as the theory of alternating currents in electricity.             Arithmetic             Arithmetic is the branch of mathematics concerned with the study of numbers and their properties. The fundamental operations of arithmetic are addition, subtraction, multiplication, and division. Raising to powers (for example, squaring or cubing a number), the extraction of roots (for example, square roots), percentages, fractions, and ratios are developed from these operations.             Forms of simple arithmetic existed in prehistoric times. In China, Egypt, Babylon, and early civilizations generally, arithmetic was used for commercial purposes, records of taxation, and astronomy. During the Dark Ages in Europe, knowledge of arithmetic was preserved in India and later among the Arabs. European mathematics revived with the development of trade and overseas exploration. Hindu-Arabic numerals replaced Roman numerals, allowing calculations to be made on paper, instead of by the abacus.             There have been many inventions and developments to make the manipulation of the arithmetic processes easier, such as the invention of logarithms by the Scottish mathematician John Napier in 1614 and of the slide rule in the period 1620–30. Since then, many forms of ready reckoners, mechanical and electronic calculators, and computers have been invented.             Modular or modulo arithmetic, sometimes known as residue arithmetic or clock arithmetic, can take only a specific number of digits, whatever the value. For example, in modulo 4 (mod 4) the only values any number can take are 0, 1, 2, or 3. In this system, 7 is written as 3 mod 4, and 35 is also 3 mod 4. Notice 3 is the residue, or remainder, when 7 or 35 is divided by 4. This form of arithmetic is often illustrated on a circle. It deals with events recurring in regular cycles, and is used in describing the functioning of gasoline engines, electrical generators, and so on. For example, in the mod 12, the answer to a question as to what time it will be in five hours if it is now ten o'clock can be expressed 10 + 5 = 3.             properties of numbers             All the properties of numbers may be deduced from the associative law, which states that the sum of a set of numbers is the same whatever the order of addition, and that the product of a set of numbers is the same whatever the order of multiplication.             commutative law The commutative law is a special case of the associative law producing commutativity where there are only two numbers in the set. For example:             distributive law The distributive law for multiplication over addition states that, given a set of numbers a, b, c, . . . and a multiplier m:             For example:             The distributive law does not apply for addition over multiplication; for example:

 

 

Page 27         identities Zero is described as the identity for addition because adding zero to any number has no effect on that number.             One is the identity for multiplication because multiplying any number by one leaves that number unchanged.             negatives Every number has a negative –n such that:             inverse Every number (except 0) has an inverse 1/n such that:             prime numbers A prime number can be divided only by 1 and itself, that is, having no other factors. There is an infinite number of primes, the first ten of which are 2, 3, 5, 7, 11, 13, 17, 19, 23, and 29 (by definition, the number 1 is excluded from the set of prime numbers). The number 2 is the only even prime because all other even numbers have 2 as a factor.             Over the centuries mathematicians have sought general methods (algorithms) for calculating primes, from Eratosthenes' sieve to programs on powerful computers.             The largest prime, 2859433–1 (258,716 digits long) was discovered in 1993. It is the thirty-third Mersenne prime. All Mersenne primes are in the form 2q–1, where q is also a prime.     Prime Numbers Prime numbers between 1 and 1,000 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997       Squares, Cubes, and Roots No. Square Cube Square root Cube root       1         1           1     1.000 1.000       2         4           8     1.414 1.260       3         9           27     1.732 1.442       4         16           64     2.000 1.587       5         25           125     2.236 1.710       6         36           216     2.449 1.817       7         49           343     2.646 1.913       8         64           512     2.828 2.000       9         81           729     3.000 2.080       10         100           1000     3.162 2.154       11         121           1331     3.317 2.224       12         144           1728     3.464 2.289       13         169           2197     3.606 2.351       14         196           2744     3.742 2.410       15         225           3375     3.873 2.466       16         256           4096     4.000 2.520       17         289           4913     4.123 2.571       18         324           5832     4.243 2.621       19           361           6859     4.359 2.668       20           400           8000     4.472 2.714       25           625           15625     5.000 2.924       30           900           27000     5.477 3.107       40           1600           64000     6.325 3.420       50           2500           125000     7.071 3.684     Prime Numbers http://www.utm.edu/research/primes/largest.html#contents         Everything you ever wanted to know about prime numbers, including the top ten recorded primes and Euclid's proof that the largest prime can never be reached.           arithmetic operations The four basic operations of arithmetic are addition, subtraction, multiplication, and division. Powers, roots, fractions, and percentages are developed from these operations. Addition is the operation of combining two numbers to form a sum; thus, 7 + 4 = 11. Subtraction involves taking one number or quantity away from another, or finding the difference between two quantities. Subtraction is neither commutative:             nor associative:             For example:

 

 

Page 28 Multiplication Table             Multiplication is usually written in the form a × b or ab, and involves repeated addition in the sense that a is added to itself b times. Multiplication obeys commutative, associative, and distributive laws (the latter over addition) and every number (except 0) has a multiplicative inverse. The number 1 is the identity for multiplication. The inverse of multiplication is division.             powers A power is represented by an exponent or index, denoted by a superior small numeral. A number or symbol raised to the power of 2—that is, multiplied by itself—is said to be squared (for example, 32, x2), and when raised to the power of 3, it is said to be cubed (for example, 23, y3). Any number to the power zero always equals 1.             Powers can be negative. Negative powers produce fractions, with the numerator as one, as a number is divided by itself, rather than being multiplied by itself, so for example 2–1 = and 3–3 = .             square roots A number that when squared (multiplied by itself) equals a given number is called a square root. For example, the square root of 25 (written Ö25) is ± 5, because 5 × 5 = 25, and (–5) × (–5) = 25. As an exponent, a square root is represented by , for example, = 4.             Negative numbers (less than 0) do not have square roots that are real numbers. Their roots are represented by complex numbers (described above), in which the square root of –1 is given the symbol i (that is, ± i2 = –1). Thus the square root of –4 is Ö[(–1) × 4] = Ö–1 × Ö4 = 2i.             fractions             A fraction (from Latin fractus ''broken") is a number that indicates one or more equal parts of a whole. Usually, the number of equal parts into which the unit is divided (denominator) is written below a horizontal line, and the number of parts comprising the fraction (numerator) is written above; thus or . Such fractions are called vulgar or simple fractions. The denominator can never be zero.             A proper fraction is one in which the numerator is less than the denominator. An improper fraction has a numerator that is larger than the denominator, for example . It can therefore be expressed as a mixed number, for example, . A combination such as is not regarded as a fraction (an object cannot be divided into zero equal parts), and mathematically any number divided by 0 is equal to infinity.             A decimal fraction has as its denominator a power of 10, and these are omitted by use of the decimal point and notation, for example 0.04, which is .

 

 

Page 29 Fractions as Decimals             The digits to the right of the decimal point indicate the numerators of vulgar fractions whose denominators are 10, 100, 1,000, and so on. Most fractions can be expressed exactly as decimal fractions ( = 0.333 . . .). Fractions are also known as rational numbers; that is, numbers formed by a ratio. Integers may be expressed as fractions with a denominator of 1, so 6 is , for example.             addition and subtraction To add or subtract with fractions, a common denominator (a number divisible by both the bottom numbers) needs to be identified. For example, for + the smallest common denominator is 12. Both the numerators and denominators of the fractions to be added (or subtracted) are then multiplied by the number of times the denominator goes into the common denominator, so is multiplied by 3 and by 2. The numerators can then be simply added or subtracted.             If whole numbers appear in the calculation they can be added/subtracted separately first.             multiplication and division All whole numbers in a division or multiplication calculation must first be converted into improper fractions. For multiplication, the numerators are then multiplied together and the denominators are then multiplied to provide the solution. For example:             In division, the procedure is similar, but the second fraction must be inverted before multiplication occurs. For example:             percentages             A percentage is way of representing a number as a fraction of 100. Thus 45 percent (45%) equals , and 45% of 20 is × 20 = 9.             In general, if a quantity × changes to y, the percentage change is 100(x–.y)/x. Thus, if the number of people in a room changes from 40 to 50, the percentage increase is (100 × 10)/40 = 25%. To express

 

 

Page 30 Percentages as Fractions or Decimals             a fraction as a percentage, its denominator must first be converted to 100– for example, = 12.5/100 = 12.5%. The use of percentages often makes it easier to compare fractions that do not have a common denominator.             To convert a fraction to a percentage on a calculator, divide numerator by denominator. The percentage will correspond to the first figures of the decimal, for example = 0.5833333 = 58.3% correct to three decimal places.             The percentage sign is thought to have been derived as an economy measure when recording in the old counting houses; writing in the numeric symbol for of a cargo would take two lines of parchment, and hence the "100" denominator was put alongside the 25 and rearranged to "%."             logarithms             The exponent or index of a number to a specified base—usually 10—is called a logarithm, or log. For example, the logarithm to the base 10 of 1,000 is 3 because 103 = 1,000; the logarithm of 2 is 0.3010 because 2 = 100.3010. The whole-number part of a logarithm is called the characteristic; the fractional part is called the mantissa.             Before the advent of cheap electronic calculators, multiplication and division could be simplified by being replaced with the addition and subtraction of logarithms.             For any two numbers × and y (where x = ba and y = bc) x × y = ba × bc = ba + c; hence we would add the logarithms of x and y, and look up this answer in antilogarithm tables.             Tables of logarithms and antilogarithms are available that show conversions of numbers into logarithms, and vice versa. For example, to multiply 6,560 by 980, one looks up their logarithms (3.8169 and 2.9912), adds them together (6.8081), then looks up the antilogarithm of this to get the answer (6,428,800). Natural or Napierian logarithms are to the base e, an irrational number equal to approximately 2.7183.             The principle of logarithms is also the basis of the slide rule. With the general availability of the electronic pocket calculator, the need for logarithms has been reduced. The first log tables (to base e) were published by the Scottish mathematician John Napier in 1614. Base-ten logs were introduced by the Englishman Henry Briggs (1561–1631) and Dutch mathematician Adriaen Vlacq (1600–1667).

 

 

Page 31         sets             A set, or class, is any collection of defined things (elements), provided the elements are distinct and that there is a rule to decide whether an element is a member of a set. It is usually denoted by a capital letter and indicated by curly brackets {}.             For example, L may represent the set that consists of all the letters of the alphabet. The symbol [member of] stands for "is a member of"; thus p [member of] L means that p belongs to the set consisting of all letters, and 4 [not member of] L means that 4 does not belong to the set consisting of all letters.             Venn diagram The sets are drawn as circles— the area of overlap between the circles shows elements that are common to each set, and thus represent a third set. Here (top) is a Venn diagram of two intersecting sets and (bottom) a Venn diagram showing the set of whole numbers from 1 to 20 and the subsets P and O of prime and odd numbers, respectively. The intersection of P and O contains all the prime numbers that are also odd.             There are various types of sets. A finite set has a limited number of members, such as the letters of the alphabet; an infinite set has an unlimited number of members, such as all whole numbers; an empty or null set has no members, such as the number of people who have swum across the Atlantic Ocean, written as {} or ø; a single-element set has only one member, such as days of the week beginning with M, written as {Monday). Equal sets have the same members; for example, if W = (days of the week} and S = {Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday), it can be said that W = S. Sets with the same number of members are equivalent sets. Sets with some members in common are intersecting sets; for example, if R = {red playing cards} and F = {face cards), then R and F share the members that are red face cards. Sets with no members in common are disjoint sets. Sets contained within others are subsets; for example, V = {vowels} is a subset of L = (letters of the alphabet). Sets and their interrelationships are often illustrated by a Venn diagram.       Set Theory http://www.history.mcs.st-and.ac.uk/~history/HistTopics/Beginnings_ofsettheory.html         Details of the beginnings of set theory. It includes biographical details of the mathematicians involved and gives a brief description of the topic.           Algebra             Algebra is the branch of mathematics in which the general properties of numbers are studied by using symbols, usually letters, to represent variables and unknown quantities. For example, the algebraic statement             is true for all values of × and y. If × = 7 and y = 3, for instance, it becomes:             An algebraic expression that has one or more variables (denoted by letters) is a polynomial equation. Algebra is used in many areas of mathematics—for example, matrix algebra and Boolean algebra (the latter is used in working out the logic for computers).             In ordinary algebra the same operations are carried on as in arithmetic, but, as the symbols are capable of a more generalized and extended meaning than the figures used in arithmetic, it facilitates calculation where the numerical values are not known, or are inconveniently large or small, or where it is desirable to keep them in an analyzed form.             Within an algebraic equation the separate calculations involved must be completed in a set order. Any elements in brackets should always be calculated first,

 

 

Page 32         followed by multiplication, division, addition, and subtraction.             algebraic terms             variable A variable is a changing quantity (one that can take various values), as opposed to a constant. For example, in the algebraic expression y = 4x3 + 2, the variables are x and y, whereas 4 and 2 are constants. Variables are generally represented as letters.             A variable may be dependent or independent. Thus if y is a function of x, written y = f(x), such that y = 4x3 + 2, the domain of the function includes all values of the independent variable × while the range (or codomain) of the function is defined by the values of the dependent variable y.             constant A constant is a fixed quantity or one that does not change its value in relation to variables (changing quantities). For example, in the algebraic expression y2 = 5x – 3, the numbers 3 and 5 are constants. In physics, certain quantities are regarded as universal constants, such as the speed of light in a vacuum.             coefficient A coefficient is the number part in front of an algebraic term, signifying multiplication. For example, in the expression 4x2 + 2xy – x, the coefficient of x2 is 4 (because 4x2 means 4 × x2), that of xy is 2, and that of x is –1 (because –1 × x = –x).             In general algebraic expressions, coefficients are represented by letters that may stand for numbers; for example, in the equation ax2 + bx + c = 0, a, b, and c are coefficients, which can take any number.             polynomial Algebraic expressions that have one or more variables (denoted by letters) are called polynomial equations. A polynomial of degree one, that is, whose highest power of x is 1, as in 2x + 1, is called a linear polynomial;             is quadratic;             is cubic.             quadratic equation A quadratic equation is a polynomial equation of second degree (that is, an equation containing as its highest power the square of a variable, such as x2). The general formula of such equations is:             in which a, b, and c are real numbers, and only the coefficient a cannot equal 0.             Some quadratic equations can be solved by factorization, or the values of x can be found by using the formula for the general solution             Depending on the value of the discriminant b2 – 4ac, a quadratic equation has two real, two equal, or two complex roots (solutions). When             there are two distinct real roots. When             there are two equal real roots. When             there are two distinct complex roots.       History and usage of quadratic equations http://www.history.mcs.st-and.ac.uk/~history/HistTopics/Quadratic_etc_equations.html         The discovery and development of quadratic equations and also biographical background information on those mathematicians responsible.           simultaneous equations If there are two or more algebraic equations that contain two or more unknown quantities that may have a unique solution, they can be solved simultaneously. For example, in the case of two linear equations with two unknown variables, such as:             the solution will be those unique values of x and y that are valid for both equations. Linear simultaneous equations can be solved by using algebraic manipulation to eliminate one of the variables. For example, both sides of equation (i) could be multiplied by 2, which gives 2x + 6y = 12. This can be added to equation (ii) to get 9y = 16, which is easily solved: y = . The variable x can now be found by inserting the known y value into either original equation and solving for x.             history of algebra             "Algebra" was originally the name given to the study of equations. In the 9th century, the Arab mathematician Muhammad ibn-Musa al-Khwarizmi used the term al-jabr for the process of adding equal quantities to both sides of an equation. When his treatise was later translated into Latin, al-jabr became "algebra" and the word was adopted as the name for the whole subject.

 

 

Page 33         The basics of algebra were familiar in ancient Babylonia (c. 18th century B.C.). Numerous tablets giving sets of problems and their answers, evidently classroom exercises, survive from that period. The subject was also considered by mathematicians in ancient Egypt, China, and India. A comprehensive treatise on the subject, entitled Arithmetica, was written in the 3rd century A.D. by Diophantus of Alexandria. In the 9th century, al-Khwarizmi drew on Diophantus" work and on Hindu sources to produce his influential work Hisab al-jabr wa'l-muqabalah/Calculation by Restoration and Reduction.             the development of symbolism From ancient times until the Middle Ages, equation-solving depended on expressing everything in words or in geometric terms. It was not until the 16th century that the modern symbolism began to be developed (notably by François Viète) in response to the growing complexity of mathematical statements which were impossibly cumbersome when expressed in words. Further research in algebra was aided not only because the symbolism was a convenient "shorthand" but also because it revealed the similarities among different problems and pointed the way to the discovery of generally applicable methods and principles.             quarternions and the idempotent law In the mid-19th century, algebra was raised to a completely new level of abstraction. In 1843, the Irish mathematician William Rowan Hamilton (1805–1865) discovered a three-dimensional extension of the number system, which he called "quaternions," in which the commutative law of multiplication is not generally true; that is, ab ¹ ba for most quaternions a and b. In 1854 George Boole applied the symbolism of algebra to logic and found it fitted perfectly except that he had to introduce a "special law" that a2 = a for all a (called the idempotent law).             algebraic structures Discoveries like this led to the realization that there are many possible "algebraic structures," which can be described as one or more operations acting on specified objects and satisfying certain laws. (Thus the number system has the operations of addition and multiplication acting on numbers and obeying the commutative, associative, and distributive laws.)             In modern terminology, an algebraic structure consists of a set, A, and one or more binary operations (that is, functions mapping A × A into A) which satisfy prescribed "axioms." A typical example is a structure which had been studied from the 18th century onward and is known as a group. This structure had turned up in the study of the solvability of polynomial equations, but it also appears in numerous other problems (for example, in geometry), and even has applications in modern physics.       The History of Algebra http://www.history.mcs.st-and.ac.uk/~history/HistTopics/Fund_theorem_of_algebra.html         The history of the theorem of algebra. The site also provides biographical details on many of the main characters involved in its development.           modern algebra The objective of modern algebra is to study each possible structure in turn, in order to establish general rules for each structure which can be applied in any situation in which the structure occurs. Numerous structures have been studied, and since 1930 a greater level of generality has been achieved by the study of "universal algebra," which concentrates on properties that are common to all types of algebraic structure.             Geometry             Geometry is concerned with the properties of space, usually in terms of plane (two-dimensional) and solid (three-dimensional) figures. The subject is usually divided into pure geometry, which embraces roughly the plane and solid geometry dealt with in Greek mathematician Euclid's Stoicheia/Elements, and analytical or coordinate geometry, in which problems are solved using algebraic methods. A third, quite distinct, type includes the non-Euclidean geometries.       Introduction to Euclidean Geometry http://ecomod.tamu.edu/~dcljr/euclid.html#intro         Thorough introduction to the principles of Euclidean geometry. There is an emphasis on the Elements, but other works associated with, or attributed to, Euclid are discussed.           pure geometry             Pure geometry is chiefly concerned with properties of figures that can be measured, such as lengths, areas, and angles, and is therefore of great practical use.             angle An angle is an amount of turn or rotation; it may be defined by a pair of rays (half-lines) that share a common endpoint but do not lie on the same line. Angles are measured in degrees (°) or radians (rads)—a complete turn or circle being 360° or 2p rads.             Angles are classified generally by their degree measures: acute angles are less than 90°; right angles are exactly 90° (a quarter turn); obtuse angles are greater than 90° but less than 180°(a straight line); reflex angles are greater than 180° but less than 360°.

 

 

Page 34         angle The four types of angle, as classified by their degree measures. No angle is classified as having a measure of 180°, as by definition such an "angle" is actually a straight line.             Angles that add up to 180° are called supplementary angles.             angles in triangles A triangle has three interior angles which together add up to 180°. In an equilateral triangle these angles are equal (60°). The exterior angles of a triangle (those produced if one side is extended beyond the triangle) are equal to the sum of the opposite internal angles. Unknown angles in a right-angled triangle can be worked out using trigonometry (see below).             angles in triangles The exterior angle of a triangle is equal to the sum of the opposite interior angles.             angles in polygons Regular polygons have three types of angle: interior, exterior, and the angle at the center (produced when a triangle is drawn inside the polygon, with the center as its apex and one side of the polygon as its base). The angle at the center is equal to the exterior angle and it is found by dividing 360° by the number of sides in the polygon. For example, the angle at the center of an octagon is 45° (360 ÷ 8).             An important idea in Euclidean geometry is the idea of congruence. Two figures are said to be congruent if they have the same shape and size (and area). If one figure is imagined as a rigid object that can be picked up, moved, and placed on top of the other so that they exactly coincide, then the two figures are congruent. Some simple rules about congruence may be stated: two line segments are congruent if they are of equal length; two triangles are congruent if their corresponding sides are equal in length or if two sides and an angle in one is equal to those in the other; two circles are congruent if they have the same radius; two polygons are congruent if they can be divided into congruent triangles assembled in the same order.             The idea of picking up a rigid object to test congruence can be expressed more precisely in terms of elementary "movements" of figures: a translation (or glide) in which all points move the same distance in the same direction (that is, along parallel lines); a rotation through a defined angle about a fixed point; a reflection (equivalent to turning the figure over).             Two figures are congruent to each other if one can be transformed into the other by a sequence of these elementary movements. In Euclidean geometry a fourth

 

 

Page 35         triangle Types of triangle.             kind of movement is also studied; this is the enlargement in which a figure grows or shrinks in all directions by a uniform scale factor. If one figure can be transformed into another by a combination of translation, rotation, reflection, and enlargement then the two are said to be similar. All circles are similar. All squares are similar. Triangles are similar if corresponding angles are equal.             triangle A triangle is a three-sided plane figure, the sum of whose interior angles is 180°. Triangles can be classified by the relative lengths of their sides. A scalene triangle has three sides of unequal length; an isosceles triangle has at least two equal sides; an equilateral triangle has three equal sides (and three equal angles of 60°).             A right-angled triangle has one angle of 90°. If the length of one side of a triangle is l and the perpendicular distance from that side to the opposite corner is h (the height or altitude of the triangle), its area A = lh.             median The median is the name given to a line from the vertex (corner) of a triangle to the midpoint of the opposite side.             hypotenuse The longest side of a right-angled triangle, opposite the right angle, is the hypotenuse. It is of particular application in the Pythagorean theorem (the square of the hypotenuse equals the sum of the squares of the other two sides), and in trigonometry where the ratios sine and cosine (see under trigonometry below) are defined as the ratios opposite/hypotenuse and adjacent/hypotenuse respectively.

 

 

Page 36         altitude The altitude of a figure is the perpendicular distance from a vertex (corner) to the base (the side opposite the vertex).             The Pythagorean theorem             The Pythagorean theorem states that in a right-angled triangle, the area of the square on the hypotenuse (the longest side) is equal to the sum of the areas of the squares drawn on the other two sides. If the hypotenuse is h units long and the lengths of the other sides are a and b, then h2 = a2 + b2.             The theorem provides a way of calculating the length of any side of a right-angled triangle if the lengths of the other two sides are known. It is also used to determine certain trigonometrical relationships such as:             The Pythagorean theorem The Pythagorean theorem for rightangled triangles is likely to have been known long before the time of Pythagoras. It was probably used by the ancient Egyptians to lay out the pyramids.             circle Technical terms used in the geometry  of the circle; the area of a circle can be seen to equal pr2 by dividing the circle into segments which form a rectangle.             circle A circle is a perfectly round shape, the path of a point that moves so as to keep a constant distance from a fixed point (the center). Each circle has a radius (the distance from any point on the circle to the center), a circumference (the boundary of the circle, part of which is called an arc), diameters (straight lines crossing the circle through the center), chords (lines joining two points on the circumference), tangents (lines that touch the circumference at one point only), sectors (regions inside the circle between two radü), and segments (regions between a chord and the circumference).             The ratio of the distance all around the circle (the circumference) to the diameter is an irrational number called p (pi), roughly equal to 3.1416. A circle of radius r and diameter d has a circumference C = pd, or C = pr, and an area A = pr2. The area of a       Pi Through The Ages http://www.history.mcs.st-and.ac.uk/~history/HistTopics/Pi_through_the_ages.html         The history of the calculation of the number pi. This site gives the figure that mathematicians from the time of Ptolemy to the present day have used for pi, and describes exactly how they calculated their figure. Also included are many historical asides, such as how calculation of pi led to a racial attack on an eminent professor in prewar Germany.

 

 

Page 37         circle can be shown by dividing it into very thin sectors and reassembling them to make an approximate rectangle. The proof of A = pr2 can be done only by using integral calculus.             pi Pi, symbol p, is the ratio of the circumference of a circle to its diameter. The value of pi is 3.1415926, correct to seven decimal places. Common approximations to pi are and 3.14, although the value 3 can be used as a rough estimation.     Pi         In 1853, the English mathematician William Shanks published the value of pi to 707 decimal places. The calculation had taken him 15 years and was surpassed only in 1945, when computations made on an early desk calculator showed that the last 180 decimal places he had calculated were incorrect.               cylinder             A cylinder is a tubular solid figure with a circular base. In everyday use, the term applies to a right cylinder, the curved surface of which is at right angles to the base.             The volume V of a cylinder is given by the formula V = pr2h, where r is the radius of the base and h is the height of the cylinder. Its total surface area A has the formula A = 2pr(h + r), where 2prh is the curved surface area, and 2pr2 is the area of both circular ends.             cylinder The volume and area of a cylinder are given by simple formulas relating the dimensions of the cylinder.             parallelogram Parallelograms are quadrilaterals (four-sided plane figures) with opposite pairs of sides equal in length and parallel, and opposite angles equal. The diagonals of a parallelogram bisect each other. Its area is the product of the length of one side and the perpendicular distance between this and the opposite side. In the special case when all four sides are equal in length, the parallelogram is known as a rhombus, and when the internal angles are right angles, it is a rectangle or square.             parallelogram Some properties of a parallelogram.       Pavilion of Polyhedreality http://www.li.net/~george/pavilion.html         A collection of images and instructions on how to make various polyhedrals, some from quite surprising materials.           coordinate geometry             Coordinate geometry is a system of geometry in which points, lines, shapes, and surfaces are represented by algebraic expressions. In plane (two-dimensional) coordinate geometry, the plane is usually defined by two axes at right angles to each other, the horizontal x-axis and the vertical y-axis, meeting at O, the origin. A point on the plane can be represented by a pair of Cartesian coordinates, which define its position in terms of its distance along the x-axis and along the y-

 

 

Page 38         axis from O. These distances are respectively the x and y coordinates of the point.             Lines are represented as equations; for example, y = 2x + 1 gives a straight line, and y = 3x2 + 2x gives a parabola (a curve). The graphs of varying equations can be drawn by plotting the coordinates of points that satisfy their equations, and joining up the points. One of the advantages of coordinate geometry is that geometrical solutions can be obtained without drawing but by manipulating algebraic expressions. For example, the coordinates of the point of intersection of two straight lines can be determined by finding the unique values of x and y that satisfy both of the equations for the lines, that is, by solving them as a pair of simultaneous equations. The curves studied in simple coordinate geometry are the conic sections (circle, ellipse, parabola, and hyperbola), each of which has a characteristic equation.             Cartesian coordinates Cartesian coordinates are components used in coordinate geometry to define the position of a point by its perpendicular distance from a set of two or more axes, or reference lines. For a two-dimensional area defined by two axes at right angles (a horizontal x-axis and a vertical y-axis), the coordinates of a point are given by its perpendicular distances from the y-axis and x-axis, written in the form (x,y). For example, a point P that lies three units from the y-axis and four units from the x-axis has Cartesian coordinates (3,4).             The Cartesian coordinate system can be extended to any finite number of dimensions (axes), and is used thus in theoretical mathematics. So coordinates can be negative numbers, or a positive and a negative, for example (–4, –7), where the point would be to the left of and below zero on the axes. In three-dimensional coordinate geometry, points are located with reference to a third, z-axis, mutually at right angles to the x and y axes.             Cartesian coordinates are named for the French mathematician René Descartes. The system is useful in creating technical drawings of machines or buildings, and in computer-aided design (CAD).             coordinate Coordinates are numbers that define the position of points in a plane or in space. In the Cartesian coordinate system, a point in a plane is charted based upon its location along intersecting horizontal and vertical axes.In the polar coordinate system, a point in a plane is defined by its distance from a fixed point and direction from a fixed line.             point A point is a basic element of geometry. Its position in the Cartesian system may be determined by its coordinates. Mathematicians have had great difficulty in defining the point, as it has no size, and is only the place where two lines meet. According to the Greek mathematician Euclid, (i) a point is that which has no part; (ii) the straight line is the shortest distance between two points.             abscissa The abscissa is the x-coordinate of a point—that is, the horizontal distance of that point from the             abscissa The abscissa of A is 4.

 

 

Page 39         vertical or y-axis. For example, a point with the coordinates (4, 3) has an abscissa of 4. The y-coordinate of a point is known as the ordinate.       Hyperbola http://www.groups.dcs.st-andrews.ac.uk/~history/Curves/Hyperbola.html         Introduction to hyperbola and links to associated curves. If your browser can handle Java code, you can experiment interactively with this curve and its associates. There are also links to mathematicians who have studied the hyperbola, to the hyperbola's particular attributes, and to related Web sites.           conic section A curve obtained when a conical surface is intersected by a plane is called a conic section. If the intersecting plane cuts both extensions of the cone, it yields a hyperbola; if it is parallel to the side of the cone, it produces a parabola. Other intersecting planes produce circles or ellipses. The Greek mathematician Apollonius wrote eight books with the title Conic Sections, which superseded previous work on the subject by Aristarchus and Euclid.             conic section The four types of curve that may be obtained by cutting a single or double right-circular cone with a plane (two-dimensional surface).       Parabola http://www.groups.dcs.st-andrews.ac.uk/~history/Curves/Parabola.html         Introduction to parabolas and links to associated curves. If your browser can handle Java code, you can experiment interactively with this curve and its associates.           topology             Topology is the branch of geometry that deals with those properties of a figure that remain unchanged even when the figure is transformed (bent, stretched)—for example, when a square painted on a rubber sheet is deformed by distorting the sheet.             Topology has scientific applications, as in the study of turbulence in flowing fluids. The topological theory,             topology Despite distortion, some properties, such as the intersection of the lines, remain unchanged.

 

 

Page 40         polyhedron The five regular polyhedra or Platonic solids.             proposed in 1880, that only four colors are required in order to produce a map in which no two adjoining countries have the same color, inspired extensive research, and was proved in 1972 by the US mathematicians Kenneth Appel and Wolfgang Haken.             The map of the London Underground system is an example of the topological representation of a network; connectivity (the way the lines join together) is preserved, but shape and size are not.             Trigonometry             Trigonometry solves problems relating to plane and spherical triangles. Its principles are based on the fixed proportions of sides for a particular angle in a right-angled triangle, the simplest of which are known as the sine, cosine, and tangent (so-called trigonometrical ratios). Trigonometry is of practical importance in navigation, surveying, and simple harmonic motion in physics.             trigonometry At its simplest level, trigonometry deals with the relationships between the sides and angles of triangles. Unknown angles or lengths are calculated by using trigonometrical ratios such as sine, cosine, and tangent.             Using trigonometry, it is possible to calculate the lengths of the sides and the sizes of the angles of a right-angled triangle as long as one angle and the length of one side are known, or the lengths of two sides. The longest side, which is always opposite to the right angle, is called the hypotenuse. The other sides are named depending on their position relating to the angle that is to be found or used: the side opposite this angle is always termed opposite and that adjacent is the adjacent. So the following trigonometrical ratios are used:             sine             The sine is the function of an angle in a right-angled triangle which is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse (the longest side). It is usually shortened to sin.             sine The sine is a function of an angle in a right-angled triangle found by dividing the length of the side opposite the angle by the length of the hypotenuse (the longest side). Sine (usually abbreviated sin) is one of the fundamentaltrigonometric ratios.             Various properties in physics vary sinusoidally; that is, they can be represented diagrammatically by a sine wave (a graph obtained by plotting values of angles against the values of their sines). Examples include simple harmonic motion, such as the way alternating current (AC) electricity varies with time.

 

 

Page 41         sine (left) The sine of an angle; (right) constructing a sine wave. The sine of an angle is a function used in the mathematical study of the triangle. If the sine of angle b is known, then the hypotenuse can be found given the length of the opposite side, or the opposite side can be found from the hypotenuse. Within a circle of unit radius (left), the height P1A1 equals the sine of angle P1OA1. This fact and the equalities below the circle allow a sine curve to be drawn, as on the right.             cosine             The cosine is the function of an angle in a right-angled triangle found by dividing the length of the side adjacent to the angle by the length of the hypotenuse (the longest side). It is usually shortened to cos.             cosine The cosine of angle b is equal to the ratio of the length of the adjacent side to the length of the hypotenuse (the longest side, opposite to the right angle).             cosine rule The cosine rule is a rule of trigonometry that relates the sides and angles of triangles. It can beused to find a missing length or angle in a triangle.             The two nonright angles of a right-angled triangle add up to 90° and are, therefore, described as complementary angles (or co-angles). If the two nonright angles are a and b, it may be seen that sin a = cos b and sin b = cos a. Therefore, the sine of each angle equals the cosine of its co-angle. For example, if the co-angles of a triangle are 30° and 60°, sin 30° = cos 60° = 0.5 sin 60° = cos 30° = 0.8660.             tangent             The tangent is a function of an acute angle in a right-angled triangle, defined as the ratio of the length of the side opposite the angle to the length of the side

 

 

Page 42         tangent The tangent of an angle is a mathematical function used in the study of right-angled triangles. If the tangent of an angle b is known, then the length of the opposite side can be found given the length of the adjacent side, or vice versa.             adjacent to it; a way of expressing the gradient of a line. It is usually written tan.             cotangent The cotangent of angle b is equal to the ratio of the length of the adjacent side to the length of the opposite side.             three-dimensional and spherical trigonometry             The methods of elementary trigonometry can be used to solve problems in three dimensions by considering triangles in different planes that have a side in common. This may also involve the use of a dropping perpendicular, that is the envisioning of an imaginary line from a point above the base that will fall vertically to the base. Spherical triangles can be solved using the trigonometric functions, though the formulas are not the same as those employed for plane triangles.             Trigonometry arose out of the study of astronomy, and was originated by the Greek astronomer Hipparchus. It was also known to early Hindu and Arab mathematicians. Ptolemy, the Alexandrian astrologer, greatly extended the subject and German astronomer Regiomontanus made it a science independent of astronomy much later on, when he began compiling trigonometrical tables in 1467.       Trigonomic Functions http://www.history.mcs.st-and.ac.uk/~history/HistTopics/Trigonometric_functions.html         History of the development of the trigonometric functions in mathematics. The site also explains the basic principles of the use of these functions and details the role they have played in the advancement of other branches of mathematics.           Calculus             Calculus (Latin ''pebble") is probably the most widely used part of mathematics. Many real-life problems are analyzed by expressing one quantity as a function of another—position of a moving object as a function of time, temperature of an object as a function of distance from a heat source, force on an object as a function of distance from the source of the force, and so on—and calculus is concerned with such functions. Calculus uses the concept of a derivative to analyze the way in which the values of a function vary.             There are several branches of calculus. Differential and integral calculus, both dealing with small quantities which during manipulation are made smaller and smaller, compose the infinitesimal calculus. Differential equations relate to the derivatives of a set

 

 

Page 43         of variables and may include the variables. Many give the mathematical models for physical phenomena such as simple harmonic motion. Differential equations are solved generally by integration, depending on their degree. If no analytical processes are available, integration can be performed numerically. Other branches of calculus include calculus of variations and calculus of errors.       Calculus http://www.history.mcs.st-and.ac.uk/~history/HistTopics/The_rise_of_calculus.html         History of the development of calculus, from the time of the Greeks to the works of Cauchy in the 19th century. Also included are several mathematical demonstrations on the use of calculus.           function             A function f is a nonempty set of ordered pairs (x, f(x)) of which no two can have the same first element. Hence, if f(x) = x2 two ordered pairs are (–2,4) and (2,4). The set of all first elements in a function's ordered pairs is called the domain; the set of all second elements is the range. In the algebraic expression             the dependent variable y is a function of the independent variable x, generally written as f(x).             Functions are used in all branches of mathematics, physics, and science generally; for example, the formula t = 2pÖ(l/g) shows that for a simple pendulum the time of swing t is a function of its length l and of no other variable quantity (p and g, the acceleration due to gravity, are constants).             limit             In an infinite sequence, the final value toward which the sequence is tending is termed the limit. For example, the limit of the sequence , , ,  . . . is 1, although no member of the sequence will ever exactly equal 1 no matter how many terms are added together.             derivative or differential coefficient             A derivative is the limit of the gradient of a chord linking two points on a curve as the distance between the points tends to zero; for a function of a single variable, y = f'(x), it is denoted by f'(x), Df(x), or dy/dx, and is equal to the gradient of the curve.             differentiation             The procedure for determining the derivative or gradient of the tangent to a curve f(x) at any point x is called differentiation. The derivative may be regarded as the limit of the expression [f(x + dx) – f(x)]/dx as dx tends to zero. Graphically, this is equivalent to the gradient (slope) of the curve represented by y = f(x) at any point x.             differentiation A mathematical procedure for determining the gradient, or slope, of the tangent to any curve f(x) at any point x.             integration Integration is the method in calculus of determining the solutions of definite or indefinite integrals. An example of a definite integral can be thought of as finding the area under a curve (as represented by an algebraic expression or function) between particular values of the function's variable. In practice, integral calculus provides scientists with a powerful tool for doing calculations that involve a continually varying quantity (such as determining the position at any given instant of a space rocket that is accelerating away from earth). Its basic principles were discovered in the late 1660s independently by the German philosopher Leibniz and the British scientist Isaac Newton.             Statistics             Statistics is concerned with the collection and interpretation of data. For example, to determine the mean age of the children in a school, a statistically acceptable answer might be obtained by calculating an average based on the ages of a representative sample, consisting, for example, of a random tenth of the pupils from each class. Probability is the branch of statistics dealing with predictions of events.             One of the most important uses of statistical theory is in testing whether experimental data support

 

 

Page 44         hypotheses or not. For example, an agricultural researcher arranges for different groups of cows to be fed different diets and records the milk yields. The milk-yield data are analyzed and the means and standard deviations of yields for different groups vary. The researcher can use statistical tests to assess whether the variation is of an amount that should be expected because of the natural variation in cows or whether it is larger than normal and therefore likely to be influenced by the difference in diet.             Correlation measures the degree to which two quantities are associated, in the sense that a variation in one quantity is accompanied by a predictable variation in the other. For example, if the pressure on a quantity of gas is increased then its volume decreases. If observations of pressure and volume are taken then statistical correlation analysis can be used to determine whether the volume of a gas can be completely predicted from a knowledge of the pressure on it.             correlation Scattergraphs showing different kinds of correlation. In this way, a causal relationship between two variables may be proved or disproved, provided there are no hidden factors.             The mean, median, and mode are different ways of finding a "typical" or "central" value of a set of data. The mean is obtained by adding up all the observed values and dividing by the number of values; it is the number which is commonly used as an average value. The median is the middle value, that is, the value which is exceeded by half the items in the sample. The mode is the value which occurs with greatest frequency, the most common value. The mean is the most useful measure for the purposes of statistical theory. The idea of the median may be extended and a distribution can be divided into four quartiles. The first quartile is the value which is exceeded by three-quarters of the items; the second quartile is the same as the median; the third quartile is the value that is exceeded by one-quarter of the items.             mean The measure of the average of a number of terms or quantities is termed the mean. The simple arithmetic mean is the average value of the quantities, that is, the sum of the quantities divided by their number. The weighted mean takes into account the frequency of the terms that are summed; it is calculated by multiplying each term by the number of times it occurs, summing the results and dividing this total by the total number of occurrences. The geometric mean of n quantities is the nth root of their product. In statistics, it is a measure of central tendency of a set of data.             median The median is the middle number of an ordered group of numbers. If there is no middle number (because there is an even number of terms), the median is the mean (average) of the two middle numbers. For example, the median of the group 2, 3, 7, 11, 12 is 7; that of 3, 4, 7, 9, 11, 13 is 8 (the average of 7 and 9).             In geometry, the term refers to a line from the vertex of a triangle to the midpoint of the opposite side.             standard deviation and other measures of dispersion             The mean is a very incomplete summary of a group of observations; it is useful to know also how closely the individual members of a group approach the mean, and this is indicated by various measures of dispersion. The range is the difference between the maximum and minimum values of the group; it is not very satisfactory as a measure of dispersion. The mean deviation is the arithmetic mean of the differences between the mean and the individual values, the differences all being taken as positive. However, the mean deviation also does not convey much useful information about a group of observations. The most useful measure of dispersion is the variance, which is the arithmetic mean of the squares of the deviations from the mean. The positive square root of the variance is called the standard deviation, a measure of the spread of data. It is usual to standardize the measurements by working in units of the standard deviation measured from the mean of the distributions, enabling statistical theories to be generalized. A standardized distribution has a mean of zero and a standard deviation of unity. Another useful measure of dispersion is the semi-interquartile range, which is one-half of the distance between the first and third quartiles, and can be considered as the average distance of the quartiles from

 

 

Page 45         the median. In many typical distributions the semi-interquartile range is about two-thirds of the standard deviation and the mean deviation is about four-fifths of the standard deviation.             standard deviation Standard deviation is a measure (symbol s or s) of the spread of data. The deviation (difference) of each of the data items from the mean is found, and their values squared. The mean value of these squares is then calculated. The standard deviation is the square root of this mean.             If n is the number of items of data, is the value of each item, and x is the mean value, the standard deviation s may be given by the formula:             where (indicates that the differences between the value of each item of data and the mean should be summed.             To simplify the calculations, the formula may be rearranged to:             As a result, it becomes necessary only to calculate Sx and Sx2.             For example, if the ages of a set of children were 4, 4.5, 5, 5.5, 6, 7, 9, and 11, Sx would be 52, x would be = = 6.5, and Sx2 would be:             Therefore, the standard deviation s would be:             probability             The likelihood, or chance, that an event will occur is its probability, which is often expressed as odds, or in mathematics, numerically as a fraction or decimal.             In general, the probability that n particular events will happen out of a total of m possible events is . A certainty has a probability of 1; an impossibility has a probability of 0. Empirical probability is defined as the number of successful events divided by the total possible number of events.             In tossing a coin, the chance that it will land "heads" is the same as the chance that it will land "tails," that is, 1 to 1 or even; mathematically, this probability is expressed as or 0.5. The odds against any chosen number coming up on the roll of a fair die are 5 to 1; the probability is or 0.1666. . . .             If two dice are rolled there are 6 × 6 = 36 different possible combinations. The probability of a double (two numbers the same) is or since there are six doubles in the 36 events: (1,1), (2,2), (3,3), (4,4), (5,5), and (6,6).             Independent events are those which do not affect each other, for example rolling two dice are independent events, as the rolling of the first die does not effect the outcome of the rolling of the second die. If events are described as mutually exclusive it means that if one happens, then it prevents the other from happening. So tossing a coin is a mutually exclusive event as it can result in a head or a tail but not both. The sum of the probabilities of mutually exclusive events is always equal to one. For example, if one has a bag containing three marbles, each of a different color, the probability of selecting each color would be .             To find out the probability of two or more mutually exclusive events occurring, their individual probabilities are added together. So, in the above example, the probability of selecting either a blue marble or a red marble is:             The probability of two independent events both occurring is smaller than the probability of one such event occurring. For example, the probability of throwing a three when rolling a die is , but the probability of throwing two threes when rolling two dice is .             Probability theory was developed by the French mathematicians Blaise Pascal and Pierre de Fermat in the 17th century, initially in response to a request to calculate the odds of being dealt various hands at cards. Today probability plays a major part in the mathematics of atomic theory and finds application in insurance and statistical studies.             chaos theory             Chaos theory or complexity theory, attempts to describe irregular, unpredictable systems—that is, systems whose behavior is difficult to predict because there are so many variable or unknown factors. Weather is an example of a chaotic system.             Chaos theory, which attempts to predict the probable behavior of such systems, based on a rapid calculation of the impact of as wide a range of elements as possible, emerged in the 1970s with the development of sophisticated computers. First developed for use in meteorology, it has also been used in such fields as quantum physics and economics.

 

 

Page 46 Playing Cards and Dice Chances Poker     Dice               (Chances with two dice and a single throw)           Hand     Number possible Odds against       Total count     Odds against       royal flush     4 649,739 to 1       2     35 to 1       straight flush     36 72,192 to 1       3     17 to 1       four of a kind     624 4,164 to 1       4     11 to 1       full house     3,744 693 to 1       5     8 to 1       flush     5,108 508 to 1       6     31 to 5       straight     10,200 254 to 1       7     5 to 1       three of a kind     54,912 46 to 1       8     31 to 5       two pairs     123,552 20 to 1       9     8 to 1       one pair     1,098,240 1.37 to 1       10     11 to 1       high card     1,302,540 1 to 1       11     17 to 1       total     2,598,960         12     35 to 1   Bridge   Dice             (Chances of consecutive winning throws)           Suit distribution in a hand     Odds against         Number of consecutive wins     By 7, 11, or point       4-4-3-2     4 to 1           5-4-2-2     8 to 1       1     1 in 49       6-4-2-1     20 to 1       2     6 in 25       7-4-1-1     254 to 1       3     3 in 25       8-4-1-0     2,211 to 1       4     1 in 17       13-0-0-0     158,753,389,899 to 1       5     1 in 34           6     1 in 70           7     1 in 141           8     1 in 287           9     1 in 582     Fractal Patterns in Nature http://polymer.bu.edu/museum/         Examination of fractal patterns in nature, including those of bacterial growth, erosion, metal deposition, and termite trails. Are they dominated by chance or are other factors involved?

 

 

Page 47         Mathematics Chronology     Mathematics Chronology c. 30000 B.C. Paleolithic peoples record tallies on bone in central Europe and France; one wolf bone has 55 cuts arranged in groups of five—the earliest counting system. c. 5000 B.C. A decimal number system is in use in Egypt. c. 3400 B.C. The first symbols for numbers, simple straight lines, are used in Egypt. c. 3000 B.C. The abacus, which uses rods and beads for making calculations, is developed in the Middle East and adopted throughout the Mediterranean. A form of the abacus is also used in China at this time.   The Sumerians of Babylon develop a sexagesimal (based on 60) numbering system. Used for recording financial transactions, the order of the numbers determines their relative, or unit value (place-value), although no zero value is used. It continues to be used for mathematics and astronomy until the 17th century A.D., and is still used for measuring angles and time. c. 1900 B.C. The Golenishev papyrus is written. It documents Egyptian Knowledge of geometry. c. 1750 B.C. The Babylonians under Hammurabi use the sexagesimal system to solve linear and quadratic algebraic equations, compile tables of square and cube roots. They are also aware of the Pythagorean property of the right-angled triangle. 876 B.C. The Hindus in India invent a symbol for zero—one of the greatest inventions in mathematics. 530 B.C. Pythagoras of Samos starts researching and teaching theories of mathematics, geometry, music, and reincarnation. A mystic as well as a mathematician, he argues that the key to the universe lies in numbers. His work leads to a number of important results, including The Pythagorean theorem of right-angled triangles and the discovery of irrational numbers (those that cannot be represented by fractions). c. 440 B.C. Greek mathematician Hippocrates of Chios writes Elements, the first compilation of the elements of geometry. c. 425 B.C. Greek mathematician Theodorus of Cyrene demonstrates that certain square roots cannot be written as fractions. c. 360 B.C. Greek mathematician and astronomer Eudoxus of Cnidus develops the theory of proportion (dealing with irrational numbers), and the method of exhaustion (for calculating the area bounded by a curve) in mathematics. c. 300 B.C. Alexandrian mathematician Euclid sets out the laws of geometry in his Stoicheion/Elements; it remains a standard text for 2,000 years. 287 B.C.– 212 B.C. The prolific Greek mathematician Archimedes of Syracuse produces a number of works on two- and three-dimensional geometry, including circles, sphere, and spirals. c. 250 B.C. Greek mathematician and inventor Archimedes provides the formulas for finding the volume of a spheres and a cylinder, arrives at an approximation of the value of pi, and creates a place-value system of notation for Greek mathematics. c. 230 B.C. Alexandrian mathematician Apollonius of Perga, writes Conics, a systematic treatise on the principles of conics in which he introduces the terms, parabola, ellipse, and hyperbola. c. 230 B.C. Greek scholar Eratosthenes of Cyrene develops a method of finding all prime numbers. Known as the sieve of Eratosthenes it involves striking out the number 1 and every nth number following the number n. Only prime numbers then remain. c. 190 B.C. Chinese mathematicians use powers of 10 to express magnitudes. 127 B.C. Greek scientist Hipparchus of Bithynia makes an early formulation of trigonometry. c. 100 B.C. Chinese mathematician begin using negative numbers. 62 Greek mathematician and engineer Hero of Alexandria writes Metrica/Measurements, containing many formulas for working out areas and volumes. 100 Greek mathematician and inventor Hero of Alexandria devises a method of representing numbers and performing simple calculating tasks using a train of gears—a primitive computer. 100–150 The classical Chinese mathematics text Jiuzhang Suanshu/Nine Chapters on the Mathematical Art is assembled. 250 Greek mathematician Diophantus of Alexandria writes Arithmetica, a study of problems in which only whole numbers are allowed as solutions. 370 Greek mathematician Hypatia writes commentaries on Diophantus and Apollonius. She is the first recorded female mathematician. 516 The Indian astronomer and mathematician Aryabhata I produces his Aryabhatiya, a treatise on quadratic equations, the value of p, and other scientific problems, in which he adds tilted epicycles to the orbits of the planets to explain their movement. 595 Decimal notation is used for numbers in India. This is the system on which our current system is based. 598–665 Indian mathematician and astronomer Brahmagupta introduces negative numbers into Indian mathematics. 780–850 Arab mathematician Muhammad ibn Musa al-

 

 

Page 48   Khwârizma introduces the Indian system of numbers to the West and give us the word "algebra," from al-jabr. c. 970 The Muslim astronomer Abu al-Wafa' discovers, and plots tables for, several new trigonometrical functions. 1040 Ahmad al-Nasawi writes on fractions, square and cubic roots, and other mathematical phenomena using Hindu (or Arabic) numerals. 1175 Arabic numerals are introduced into Europe with Gerard of Cremona's translation of the Egyptian astronomer Ptolemy's astronomical work the Almagest. 1202 Italian mathematician Fibonacci wirtes Liber abaci/The Book of the Abacus, which introduces the famous sequence of numbers now called the Fibonacci sequence. 1335 The English abbot of st. Albans Richard of Wallingford writes Quadripartitum de sinibus demonstratis, the first original Latin treatise on trigonometry. 1364 French astronomer and bishop Nicole d'Oresme writes Latitudes of Forms, an early work on coordinate systems. 1533 Flemish cartographer and mathematician Gemma Frisius publishes a method for accurate surveying using trigonometry. 1545 The Italian mathematician Girolamo Cardano publishes a formula that will solve any cubic equation, discovered by his student Niccolo Tartaglia. 1591 French mathematician François Viète uses letters of the alphabet to represent unknown quantities. Before this, equations had been written out in long descriptive sentences. 1614 Scottish mathematician John Napier invents logarithms, a method for doing difficult calculations quickly. 1617 Dutch mathematician and physicist Willibrord Snell establishes the technique of trigonometrical triangulation to improve the accuracy of cartographic measurements. 1617 Scottish mathematician John Napier, inventor of the log table, devises a system of numbered sticks, called Napier's bones, to aid complex calculations. 1622 English mathematician William Oughtred invents an early form of circular slide rule, adapting the principle behind Scottish mathematician John Napier's "bones." 1639 French mathematician Girard Desargues begins the study of projective geometry, which considers what happens to shapes when they are projected onto a screen. 1642 French mathematician Blaise Pascal, aged only 19, builds an adding machine to help his father, the Intendant of Rouen, with tax calculations. 1642–1727 English scientist Isaac Newton lays the foundations of modern mathematics and physics throughout his lifetime. 1653 French mathematician Blaise Pascal publishes his "triangle" of numbers. This has many applications in arithmetic, algebra, and combinatorics (the study of counting combinations). 1657 Pierre de Fermat claims to have proved a certain theorem, but leaves no details of his proof. Known as Fermat's last theorem, it is finally proved by English mathematician Andrew Wiles in 1994. 1660 Newton begins work on the calculus, a fundamental tool in physics for studying rates of change. 1673 German mathematician Gottfried von Leibniz presents a calculating machine to the Royal Society, London, England. It is the most advanced yet, capable of multiplication, division, and extracting roots. 1676 Newton proves the binomial theorem, a basic tool in solving algebraic equations. 1679 German mathematician Gottfried von Leibniz introduces binary arithmetic, in which only two symbols are used to represent all numbers. It will eventually pave the way for computers. 1684 Leibniz invents the differential calculus, a fundamental tool in studying rates of change. 1690 Swiss mathematician Jacques Bernoulli uses the word "integral" for the first time to refer to the area under a curve. 1694 Swiss mathematician Jean Bernoulli discovers L'Hôpital's rule for determining the correct value of certain ratios. 1707 French mathematician Abraham de Moivre uses trigonometric functions to understand complex numbers for the first time. 1713 Jacques Bernoulli's book Ars conjectandi/The Art of Conjecture is the first to deal with probability. 1717 Jean Bernoulli declares that the principle of virtual displacement is applicable to all cases of equilibrium. 1718 Jacques Bernoulli's work on the calculus of variations (the study of functions that are close to their maximum and minimum values) is published posthumously. 1722 De Moivre proposes an equation that is fundamental to the development of complex numbers. 1724 Italian mathematician Jacapo Riccati propounds his equation, an important type of differential equation. 1730 De Moivre propounds theorems of trigonometry concerning imaginary quantities. 1733 De Moivre describes the normal distribution curve.

 

 

Page 49 1742 German mathematician Christian Goldbach conjectures that every even number greater than two can be written as the sum of two prime numbers. Goldbach's conjecture has not yet been proved. 1746 French mathematician Jean d'Alembert develops the theory of complex numbers. 1748 Swiss mathematician Leonhard Euler publishes Analysis Infinitorum/Analysis of Infinities, an introduction to pure analytical mathematics. He introduces a formula linking the value of pi to the square root of –1. 1763 The Reverend Thomas Bayes, The English mathematician and theologian, publishes "An Essay Towards Solving a Problem in the Doctrine of Chances." This includes Baye's Theorem, which is an important theorem in statistics. 1767 German mathematician Johann Heinrich Lambert proves that the value of pi cannot be written exactly as a fraction. 1772 Italian-born French mathematician Joseph-Louis Lagrange proves that every whole number can be written as the sum of four square numbers. 1789 The French mathematician Baron Augustine-Louis Cauchy completes his lifelong mathematical research, having made great advances in analysis, probability, and group theory. 1797 Lagrange introduces the modern notation for derivatives. 1798 Norwegian mathematician Caspar Wessel introduces the vector representation of complex numbers. 1799 The German mathematician Karl Friedrich Gauss proves the fundamental theorem of algebra that every algebraic equation has as many solutions as the exponent of the highest term. 1810 French mathematician Jean-Baptiste-Joseph Fourier publishes his method of representing functions by a series of trigonometric functions. 1812 French mathematician Pierre-Simon Laplace describes the mathematical tools he has invented for predicting the probabilities of occurrence of natural events; this is the first complete theoretical account of probability. 1815 English physician and philologist Peter Roget invents the "log-log" slide rule. c. 1820 Gauss introduces the normal distribution curve ("Gaussian distribution")—a basic statistical tool. 1820 French mathematician Charles-Thomas de Colmar develops the first mass-produced calculator—the "arithmometer." 1822 French mathematician Jean-Victor Poncelet systematically develops the principles of projective geometry. 1822 Fourier introduces a technique now known as Fourier analysis, which has widespread applications in mathematics, physics, and engineering. 1823 English mathematician Charles Babbage begins construction of the "difference" engine, a machine for calculating logarithms and trigonometric functions. 1824 German mathematician and astronomer Friedrich Wilhelm Bessel discovers a class of functions, now called Bessel functions, that arise in many areas of physics. 1824 Swiss mathematician Jakob Steiner develops inversive geometry. 1827 Gauss introduces the subject of differential geometry that describes features of surfaces by analyzing curves that lie on it—the intrinsic-surface theory. 1828 English mathematician George Green introduces a theorem that enables volume integrals to be calculated in terms of surface integrals. 1828 Norwegian mathematician Niels Abel begins the study of elliptic functions. 1829 French mathematician Evariste Galois invents group theory, which helps use ideas of symmetry to solve equations. 1829 Russian mathematician Nikolay Ivanovich Lobachevsky develops hyperbolic geometry, in which a plane is regarded as part of a hyperbolic surface shaped like a saddle. It is the beginning of non-Euclidean geometry. 1832 Swiss mathematician Jakob Steiner founds synthetic geometry with the publication of Systematic Development of the Dependency of Geometrical Forms on One Another. 1836 Poncelet introduces the use of mathematics to machine design. 1837 French mathematician Siméon-Denis Poisson establishes the rules of probability and describes the Poisson distribution. 1843 English mathematician Arthur Cayley is the first person to investigate spaces with more than three dimensions. 1843 Irish mathematician William Rowan Hamilton invents quaternions, which make possible the application of arithmetic to three-dimensional objects. 1844 French mathematician Joseph Liouville finds the first transcendental numbers—numbers that cannot be expressed as the roots of an algebraic equation with rational coefficients. 1845 Cayley publishes Theory of Linear Transformations, which lays the foundation of the school of pure mathematics. 1845 Augustine Cauchy proves the fundamental theorem of group theory, subsequently known as Cauchy's theorem. 1847 English mathematician Augustus de Morgan proposes two laws of logic that are now known as de Morgan's laws. 1847 The English mathematician George Boole

 

 

Page 50   publishes The Mathematical Analysis of Logic, in which he shows that the rules of logic can be treated mathematically. Boole's work lays the foundation of computer logic. 1854 Boole outlines his system of symbolic logic now known as Boolean algebra. 1854 Cayley makes important advances in group theory. 1854 German mathematician George Friedrich Bernhard Riemann formulates his concept of non-Euclidean geometry in On the Hypotheses forming the Foundation of Geometry. 1857–1936 English mathematician Karl Pearson introduces a number of fundamental concepts to the study of statistics. 1858 Cayley invents matrices (rectangular arrays of numbers) and studies their properties. 1859 French artillery officer Amédée Mannheim invents the first modern slide rule that has a cursor or indicator. 1859 Riemann makes a conjecture about a function called the zeta function. Riemann's hypothesis is still unproved, but is an important key to understanding prime numbers. 1865 German mathematician and physicist Julius Plückner invents line geometry. 1871 German mathematician Karl Theodor Wilhelm Weierstrass discovers a curve that, while continuous, has no definable gradient at any point. 1872 German mathematician Richard Dedekind demonstrates how irrational numbers (those that cannot be written as a fraction) may be defined formally. 1874 German mathematician Georg Cantor is the first person rigorously to describe the notion of infinity. 1880 French mathematician Jules-Henri Poincaré publishes important results on automorphic functions, a subject of great importance in modern algebra. 1881 English mathematician John Venn introduces the idea of using pictures of circles to represents sets, subsequently known as Venn diagrams. 1881 US scientist Josiah Willard Gibbs develops the theory of vectors in three dimensions. 1882 Ferdinand Lindemann proves p is a transcendental number. 1882 German mathematician Carl Louis Ferdinand von Lindemann proves that it is impossible to construct a square with the same area as a given circle using a ruler and compass. 1892 German mathematician Georg Cantor demonstrates that there are different kinds of infinity. 1895 Poincaré publishes the first paper on topology, often referred to as "rubber sheet geometry." 1896 The prime number theorem is proved independently by mathematicians Jacques-Salomon Hadamard of France and Charles-Jean de la Vallée-Poussin of Belgium. This theorem gives an estimate of the number of primes there are up to a given number. 1899 German mathematician David Hilbert publishes Grundlagen der Geometrie/Foundations of Geometry, which provides a rigorous basis for geometry. 1902 U.S. physicist J. Willard Gibbs publishes Elementary Principles of Statistical Mechanics, in which he develops the mathematics of statistical mechanics. 1906 Russian mathematician Andrey Andreyevich Markov studies random processes that are subsequently known as Markov chains. 1908 German mathematician Ernst Zermelo publishes Untersuchungen über die Grundlagen der Mengenlehre/Investigations on the Foundations of Set Theory, which forms the basis of modern set theory. 1910 English philosophers Bertrand Russell and

 

 

Page 51   Alfred North Whitehead publish the first volume of their three-volume Principia Mathematica/Principles of Mathematics, in which they attempt to derive the whole of mathematics from a logical foundation. The last volume appears in 1913. 1922 Polish mathematician Stefan Banach begins his work on a development of vector spaces, an important tool in general analysis. 1931 Austrian mathematician Kurt Gödel publishes "Gödel's proof." His proof questions the possibility of establishing dependable axioms in mathematics, showing that any formula strong enough to include the laws of arithmetic is either incomplete or inconsistent. 1931 Gödel proves that in any mathematical system such as arithmetic, there are statements that cannot be proved true or false. 1935 U.S. mathematician Alonzo Church invents lambda calculus, a mathematical method for representing mechanical computations. 1936 British mathematician Alan Turing supplies the theoretical basis for digital computers by describing a machine, now known as the Turing machine, capable of universal rather than special-purpose problem solving. 1937–39 U.S. mathematician and physicist John V. Atanasoff invents an electromechanical digital computer for solving systems of linear equations. It uses punched cards and is the first electronic calculator using electronic vacuum tubes. 1948 U.S. mathematician Claude Elwood Shannon invents information theory, a mathematical treatment of information that has important applications in computer science and communications. 1950 German-born U.S. logician Rudolf Carnap publishers Logical Foundations of Probability. 1950 Russian mathematician Andrey Nikolaevich Kolmogorov presents the first formal treatment of probability in Foundations of the Theory of Probability. 1961 U.S. meteorologist Edward Lorenz discovers a mathematical system with chaotic behavior, leading to a new branch of mathematics known as chaos theory. 1972 French mathematician René Frédéric Thom formulates catastrophe theory, an attempt to describe biological proceses mathematically. 1975 U.S. mathematician Mitchell Fingelbaum discovers a new fundamental constant (approximately 4.6692016), which plays an important part in chaos theory. 1976 U.S. mathematicians Kenneth Appel and Wolfgang Haken use a computer to prove the four-color problem—that the minimum number of colors needed to color a map such that no two adjacent sections have the same color is four. The proof takes 1,000 hours of computer time and hundreds of pages. 1980 Mathematicians worldwide complete the classification of all finite and simple groups, a task that has taken over 100 mathematicians more than 35 years to complete. The results take up more than 14,000 pages in mathematical journals. 1980 Polish-born French mathematician Benoit Mandelbrot discovers fractals. The Mandelbrot set is a spectacular shape with a fractal boundary (a boundary of infinite length enclosing a finite area). 1994 English mathematician Andrew Wiles, at Princeton University, NJ, proves Fermat's last theorem, a problem that had remained unsolved since 1657. 1998 Cambridge University professors Richard Borchers and Tim Gowers win Fields Medals in Mathematics for work in vertex algebra and probabilistic number theory, at the International Congress of Mathematicians in Berlin, Germany.

 

 

Page 52         Biographies             Alembert, Jean le Rond d' (1717–1783) French mathematician, encyclopedist, and theoretical physicist. He framed several theorems and principles—notably d'Alembert's principle—in dynamics and celestial mechanics, and devised the theory of partial differential equations. The principle that now bears his name was first published in his Traité de dynamique (1743), and was an extension of the third of Isaac Newton's laws of motion. From the early 1750s, together with other mathematicians such as Joseph Lagrange and Pierre Laplace, he applied calculus to celestial mechanics. In particular, he worked out in 1754 the theory needed to set Newton's discovery of the precession of the equinoxes on a sound mathematical basis, and explained the phenomenon of the oscillation of the earth's axis.             Apollonius of Perga (c. 262–c. 190 B.C.) Greek mathematician, called ''the Great Geometer." In his eight-volume work Konica/The Conics, he showed that a plane intersecting a cone will generate an ellipse, a parabola, or a hyperbola, depending on the angle of intersection. The first four books consisted of an introduction and a statement of the state of mathematics provided by his predecessors. In the last four volumes, Apollonius put forth his own important work on conic sections, the foundation of much of the geometry still used today in astronomy, ballistic science, and rocketry.             Archimedes (c. 287–212 B.C.) Greek mathematician who made major discoveries in geometry, hydrostatics, and mechanics, and established the sciences of statics and hydrostatics. He formulated a law of fluid displacement (Archimedes' Principle), and is credited with the invention of the Archimedes screw, a cylindrical device for raising water. His method of finding mathematical proof to substantiate experiment and observation became the method of modern science in the High Renaissance.             Archimedes wrote many mathematical treatises. His approximation for the value for p was more accurate than any previous estimate—the value lying between 223/71 and 220/70. The average of these two numbers is less than 0.0003 different from the modern approximation for p. He also examined the expression of very large numbers, using a special notation to estimate the number of grains of sand in the universe. Although the result, 1063, was far from accurate, he demonstrated that large numbers could be considered and handled effectively. Archimedes also evolved methods to solve cubic equations and to determine square roots by approximation. His formulas for the determination of the surface areas and volumes of curved surfaces and solids anticipated the development of integral calculus, which did not come for another 2,000 years.             Barrow, Isaac (1630–1677) British mathematician, theologian, and classicist. His Lectiones geometricae (1670) contains the essence of the theory of calculus, which was later expanded by Isaac Newton and Gottfried Leibniz.             Bernoulli, Daniel (1700–1782) Swiss mathematical physicist. He made important contributions to trigonometry and differential equations (differentiation). Among his achievements in mathematics, he demonstrated how the differential calculus could be used in problems of probability. He did pioneering work in trigonometrical series and the computation of trigonometrical functions. He also showed the shape of the curve known as the lemniscate. In hydrodynamics he proposed Bernoulli's principle, which states that the pressure of a moving fluid decreases the faster it flows—an early formulation of the idea of conservation of energy.             Bernoulli, Jakob (1654–1705) Swiss mathematician who with his brother Johann pioneered the German mathematician Gottfried Leibniz's calculus. Jakob used calculus to study the forms of many curves arising in practical situations, and studied mathematical probability (Ars conjectandi 1713); Bernoulli numbers (a series of complex fractions) are named for him.             Bernoulli, Johann (1667–1748) Swiss mathematician who with his brother Jakob pioneered the German mathematician Gottfried Leibniz's calculus. He was the father of Daniel Bernoulli. Johann also contributed to many areas of applied mathematics, including the problem of a particle moving in a gravitational field. He found the equation of the catenary in 1690 and developed exponential calculus in 1691.             Bolyai, János (1802–1860) Hungarian mathematician, one of the founders of non-Euclidean geometry. He was the first to see Euclidean geometry as only one case, and that others were possible. By about 1820 he had become convinced that a proof of Euclid's postulate about parallel lines was impossible; he began instead to construct a geometry which did not depend upon Euclid's axiom. He developed his formula relating the angle of parallelism of two lines with a term characterizing the line. In his new theory Euclidean space was simply a limiting case of the new space, and Bolyai introduced his formula to express what later became known as the space constant.             Boole, George (1815–1864) English mathematician. His work The Mathematical Analysis of Logic (1847) established the basis of modern mathematical logic, and his Boolean algebra can be used in designing computers. His system is essentially two-valued. By subdividing objects into separate classes, each with a given property, his algebra makes it possible to treat different classes according to the presence or absence of the same property. Hence it involves just two numbers, 0 and 1—the binary system used in the computer.             Calderón, Alberto P (1920–1998) Argentine mathematician who specialized in Fourier analysis and partial differential equations. Together with mathematician Antoni Zygmund, he devised the Calderón-Zygmund theory of singular integrals.             Cantor, Georg Ferdinand Ludwig Philipp (1845–1918) German mathematician. He defined real numbers and produced a treatment of irrational numbers using a series of transfinite numbers. Investigating sets of the points of convergence of the Fourier series (which enables functions to be represented by trigonometric series), Cantor derived the theory of sets that is the basis of modern mathematical analysis. His work contains many definitions and theorems in topology. For the theory of sets, he had to arrive at a definition of infinity, and also therefore consider the transfinite; for this he used the ancient term "continuum." He showed that within the infinite there are countable sets and there are sets having the power of a continuum, and proved that for every set there is another set of a higher power.

 

 

Page 53         Cauchy, Augustin Louis, Baron de (1789–1857) French mathematician who employed rigorous methods of analysis. His prolific output included work on complex functions, determinants, and probability, and on the convergence of infinite series. In calculus, he refined the concepts of the limit and the definite integral. Cauchy has the credit for 16 fundamental concepts and theorems in mathematics and mathematical physics, more than any other mathematician. His work provided a basis for the calculus. He provided the first comprehensive theory of complex numbers, which contributed to the development of mathematical physics and, in particular, aeronautics.             Condorcet, Marie Jean Antoine Nicolas de Caritat, Marquis de Condorcet (1743–1794) French philosopher, mathematician, and politician. As a mathematician he made important contributions to the theory of probability.             Descartes, René (1596–1650) French philosopher and mathematician. He believed that commonly accepted knowledge was doubtful because of the subjective nature of the senses, and attempted to rebuild human knowledge using as his foundation the dictum cogito ergo sum ("I think, therefore I am"). He also believed that the entire material universe could be explained in terms of mathematical physics, and founded coordinate geometry as a way of defining and manipulating geometrical shapes by means of algebraic expressions. Cartesian coordinates, the means by which points are represented in this system, are named after him. His great work in mathematics was La Géométrie/ Geometry (1637). Although not the first to apply algebra to geometry, he was the first to apply geometry to algebra. He was also the first to classify curves systematically, separating "geometric curves" (which can be precisely expressed as an equation) from "mechanical curves" (which cannot).             Diophantus (lived A.D. 250) Greek mathematician in Alexandria whose Arithmetica is one of the first known works on problem solving by algebra, in which both words and symbols are used. His main mathematical study was in the solution of what are now known as "indeterminate" or "Diophantine" equations—equations that do not contain enough facts to give a specific answer but enough to reduce the answer to a definite type. These equations have led to the formulation of the theory of numbers, regarded as the purest branch of present-day mathematics. In the solution of equations Diophantus was the first to abbreviate the expression of his calculations by means of a symbol representing the unknown quantity.             Eratosthenes (c. 276–c. 194 B.C.) Greek geographer and mathematician whose map of the ancient world was the first to contain lines of latitude and longitude, and who calculated the earth's circumference with an error of about 10%. His mathematical achievements include a method for duplicating the cube, and for finding prime numbers (Eratosthenes' sieve).             Euclid (c. 330–c. 260 B.C.) Greek mathematician who wrote the Stoicheial Elements in 13 books, nine of which deal with plane and solid geometry and four with number theory. His great achievement lay in the systematic arrangement of previous mathematical discoveries and a methodology based on axioms (statements assumed to be true), definitions, and theorems. He used two main styles of presentation: the synthetic (in which one proceeds from the known to the unknown via logical steps) and the analytical (in which one posits the unknown and works toward it from the known, again via logical steps). Both methods were based on axioms and from which mathematical propositions, or theorems, were deduced.             Euler, Leonhard (1707–1783) Swiss mathematician. He developed the theory of differential equations and the calculus of variations, developed spherical trigonometry, and demonstrated the significance of the coefficients of trigonometric expansions; Euler's number (e, as it is now called) has various useful theoretical properties and is used in the summation of particular series.             Fermat, Pierre de (1601–1665) French mathematician who, with Blaise Pascal, founded the theory of probability and the modern theory of numbers. Fermat also made contributions to analytical geometry. In 1657 he published a series of problems as challenges to other mathematicians, in the form of theorems to be proved. Fermat's last theorem states that equations of the form xn+ yn = zn where x, y, z, and n are all integers have no solutions if n > 2. In 1993, English mathematician Andrew Wiles announced a proof; this turned out to be premature, but he put forward a revised proof in 1994.             Fibonacci, Leonardo, also known as Leonardo of Pisa (c. 1170–c. 1250) Italian mathematician. He published Liber abaci/The Book of the Calculator (1202), which was instrumental in the introduction of Arabic notation into Europe. From 1960, interest increased in Fibonacci numbers, in their simplest form a sequence in which each number is the sum of its two predecessors (1, 1, 2, 3, 5, 8, 13, . . .). Fibonacci also published Practica geometriae (1220), in which he used algebraic methods to solve many arithmetical and geometrical problems.             Fourier, Jean Baptiste Joseph (1768–1830) French applied mathematician whose formulation of heat flow in 1807 contains the proposal that, with certain constraints, any mathematical function can be represented by trigonometrical series. This principle forms the basis of Fourier analysis, used today in many different fields of physics. His idea is embodied in his Théorie analytique de la chaleur/The Analytical Theory of Heat (1822). Light, sound, and other wavelike forms of energy can be studied using Fourier's method, a developed version of which is now called harmonic analysis. Fourier laid the groundwork for the later development of dimensional analysis and linear programming. He also investigated probability theory and the theory of errors.             Galois, Evariste (1811–1832) French mathematician who originated the theory of groups and greatly extended the understanding of the conditions in which an algebraic equation is solvable. What has come to be known as the Galois theorem demonstrated the insolubility of higher-than-fourth-degree equations by radicals. Galois theory involved groups formed from the arrangements of the roots of equations and their subgroups, which he fitted into each other rather like Chinese boxes.             Gauss, Carl Friedrich (1777–1855) German mathematician who worked on the theory of numbers, non-Euclidean geometry, and the mathematical development of electric and magnetic theory. A method of neutralizing a magnetic field, used to protect ships from magnetic mines, is called "degaussing." In statistics, the normal distribution curve, which he studied, is sometimes known as the Gaussian distribution.

 

 

Page 54         Disquisitiones arithmeticae (1801) summed up Gauss's work in number theory and formulated concepts and questions that are still relevant today.             Gödel, Kurt (1906–1978) Austrian-born U.S. mathematician and philosopher. In his paper, "On formally undecidable propositions of Principia Mathematica and related systems" (1931), he proved that a mathematical system always contains statements that can be neither proved nor disproved within the system; in other words, as a science, mathematics can never be totally consistent and totally complete. He worked on relativity, constructing a mathematical model of the universe that made travel back through time theoretically possible.             Gunter, Edmund (1581–1626) English mathematician. He is reputed to have invented a number of surveying instruments as well as the trigonometrical terms "cosine" and "cotangent." His measuring instruments include Gunter's Chain, the 22-yard-long, 100-link chain used by surveyors; Gunter's Line, the forerunner of the slide-rule; Gunter's Scale, a two-foot rule with scales of chords, tangents and logarithmic lines for solving navigational problems, and the portable Gunter's Quadrant.             Hilbert, David (1862–1943) German mathematician, philosopher, and physicist whose work was fundamental to 20th-century mathematics. He founded the formalist school with Grundlagen der Geometrie/Foundations of Geometry (1899), which was based on his idea of postulates. He attempted to put mathematics on a logical foundation through defining it in terms of a number of basic principles, which Kurt Gödel later showed to be impossible. In 1900 he proposed a set of 23 problems for future mathematicians to solve, and gave 20 axioms to provide a logical basis for Euclidean geometry.             Studying algebraic invariants, Hilbert had by 1892 not only solved all the known central problems of this branch of mathematics, he had introduced sweeping developments and new areas for research, particularly in algebraic topology.             Khwarizmi, al-, Muhammad ibn-Musa (c. 780–c. 850) Persian mathematician. He wrote a book on algebra, from part of whose title (al-jabr) comes the word "algebra," and a book in which he introduced to the West the Hindu-Arabic decimal number system. He compiled astronomical tables and was responsible for introducing the concept of zero into Arab mathematics. The word "algorithm" is a corruption of his name.             Kovalevskaia, Sofya Vasilevna (1850–1891) Russian mathematician who worked on partial differential equations and Abelian integrals. In 1886 she won the Prix Bordin of the French Academy of Sciences for a paper on the rotation of a rigid body about a point, a problem the 18th-century mathematicians Leonhard Euler and Joseph Lagrange had both failed to solve.             Lagrange, Joseph Louis (1736–1813) Italian-born French mathematician. His Mécanique analytique (1788) applied mathematical analysis, using principles established by Isaac Newton, to such problems as the movements of planets when affected by each other's gravitational force. He presided over the commission that introduced the metric system in 1793. Lagrange proved some of Pierre de Fermat's theorems, which had remained unproven for a century.             Laplace, Pierre Simon, Marquis de Laplace (1749–1827) French astronomer and mathematician. Among his mathematical achievements was the development of probability theory. In "Théorie des attractions des sphéroïdes et de la figure des planètes" (1785) he introduced the potential function and the Laplace coefficients, both of them useful as a means of applying analysis to problems in physics.             Leibniz, Gottfried Wilhelm (1646–1716) German mathematician, philosopher, and diplomat. Independently of, but concurrently with, the English scientist Isaac Newton, he developed the branch of mathematics known as calculus and was one of the founders of symbolic logic. Free from all concepts of space and number, his logic was the prototype of future abstract mathematics. Leibniz is due the credit for first using the infinitesimals (very small quantities that were precursors of the modern idea of limits) as differences. He devised a notation for integration and differentiation that was so much more convenient than Newton's fluxions that it remains in standard use today. He also designed a calculating machine, completed about 1672, which was able to multiply, divide, and extract roots.             Lobachevsky, Nikolai Ivanovich (1792–1856) Russian mathematician who founded non-Euclidean geometry, concurrently with, but independently of, Karl Gauss in Germany and János Bolyai in Hungary. Lobachevsky published the first account of the subject in 1829, but his work went unrecognized until Georg Riemann's system was published.             In Euclid's system, two parallel lines will remain equidistant from each other, whereas in Lobachevskian geometry, the two lines will approach zero in one direction and infinity in the other. In Euclidean geometry the sum of the angles of a triangle is always equal to the sum of two right angles; in Lobachevskian geometry, the sum of the angles is always less than the sum of two right angles. In Lobachevskian space, also, two geometric figures cannot have the same shape but different sizes.             Mandelbrot, Benoit B (1924– ) Polish-born French mathematician who coined the term fractal to describe geometrical figures in which an identical motif repeats itself on an ever-diminishing scale. The concept is associated with chaos theory. Mandelbrot's research has provided mathematical theories for erratic chance phenomena and self-similarity methods in probability. He has also carried out research on sporadic processes, thermodynamics, natural languages, astronomy, geomorphology, computer art and graphics, and the fractal geometry of nature.             Markov, Andrei Andreyevich (1856–1922) Russian mathematician, formulator of the Markov chain, an example of a stochastic (random) process. A Markov chain may be described as a chance process that possesses a special property, so that its future may be predicted from the present state of affairs just as accurately as if the whole of its past history were known. Markov chains are now used in the social sciences, atomic physics, quantum theory, and genetics.             Möbius, August Ferdinand (1790–1868) German mathematician and theoretical astronomer, discoverer of the Möbius strip and considered one of the founders of topology. In 1818 he formulated his barycentric calculus, a mathematical system in which numerical coefficients were

 

 

Page 55         assigned to points. The position of any point in the system could be expressed by varying the numerical coefficients of any four or more noncoplanar points. He also discovered the Möbius net, later of value in the development of projective geometry; the Möbius tetrahedra, two tetrahedra that mutually circumscribe and inscribe each other, which he described in 1828; and the Möbius function in number theory, published in 1832.             Napier, John, 8th Laird of Merchiston (1550–1617) Scottish mathematician who invented logarithms in 1614 and "Napier's bones," an early mechanical calculating device for multiplication and division. It was Napier who first used and then popularized the decimal point to separate the whole number part from the fractional part of a number.             Oughtred, William (1575–1660) English mathematician, credited as the inventor of the slide rule in 1622. His major work Clavis mathematicae/The Key to Mathematics (1631) was a survey of the entire body of mathematical knowledge of his day. It introduced the "x" symbol for multiplication, as well as the abbreviations "sin" for sine and "cos" for cosine.             Pascal, Blaise (1623–1662) French philosopher and mathematician. He contributed to the development of hydraulics, calculus, and the mathematical theory of probability. His work in mathematics widened general understanding of conic sections, introduced an algebraic notational system that rivaled that of Descartes, and made use of the arithmetical triangle (called Pascal's triangle) in the study of probabilities. Between 1642 and 1645, Pascal constructed a machine to carry out the processes of addition and subtraction, and then organized the manufacture and sale of these first calculating machines.             Together with Pierre de Fermat, Pascal studied two specific problems of probability: the first concerned the probability that a player will obtain a certain face of a die in a given number of throws; and the second was to determine the portion of the stakes returnable to each player of several if a game is interrupted. Pascal used the arithmetical triangle to derive combinational analysis. Pascal's triangle is a triangular array of numbers in which each number is the sum of the pair of numbers above it. In general the nth (n = 0, 1, 2, . . .) row of the triangle gives the binomial coefficients nCr, with r = 0, 1, . . ., n. In 1657–59 Pascal also perfected his "theory of indivisibles"—the forerunner of integral calculus which enabled him to study problems involving infinitesimals, such as the calculations of areas and volumes.             Pearson, Karl (1857–1936) English statistician who followed the English scientist Francis Galton (1822–1911) in introducing statistics and probability into genetics. He introduced the term "standard deviation" into statistics. In 1900 he introduced the c2 (chi-squared) test to determine whether a set of observed data deviates significantly from what would have been predicted by a "null hypothesis" (that is, totally at random). He demonstrated that it could be applied to examine whether two hereditary characteristics (such as height and hair color) were inherited independently. Pearson's discoveries included the Pearson coefficient of correlation (1892), the theory of multiple and partial correlation (1896), the coefficient of variation (1898), work on errors of judgment (1902), and the theory of random walk (1905).             Poincaré, Jules Henri (1854–1912) French mathematician who developed the theory of differential equations and was a pioneer in relativity theory. He suggested that Isaac Newton's laws for the behavior of the universe could be the exception rather than the rule. However, the calculation was so complex and time-consuming that he never managed to realize its full implication. He published the first paper devoted entirely to topology (the branch of geometry that deals with the unchanged properties of figures), and developed several new mathematical techniques, including the theories of asymptotic expansions and integral invariants, and the new subject of topological dynamics.             Poisson, Siméon Denis (1781–1840) French applied mathematician and physicist. In probability theory he formulated the Poisson distribution. Poisson's ratio in elasticity is the ratio of the lateral contraction of a body to its longitudinal extension. The ratio is constant for a given material. Much of Poisson's work involved applying mathematical principles in theoretical terms to contemporary and prior experiments in physics, particularly with reference to electricity, magnetism, heat, and sound. Poisson was also responsible for a formulation of the "law of large numbers."       Pythagoras http://www.utm.edu/research/iep/p/pythagor.htm         Profile of the legendary mathematician, scientist, and philosopher Pythagoras. An attempt is made to disentangle the known facts of his life from the mass of legends about him.           Pythagoras (c. 580–500 B.C.) Greek mathematician and philosopher who formulated The Pythagorean theorem (the square of the hypotenuse equals the sum of the squares of the other two sides). Much of his work concerned numbers, to which he assigned mystical properties. For example, he classified numbers into triangular ones (1, 3, 6, 10, . . .), which can be represented as a triangular array, and square ones (1, 4, 9, 16, . . .), which form squares. He also observed that any two adjacent triangular numbers add to a square number (for example, 1 + 3 = 4; 3 + 6 = 9; 6 + 10 = 16).             Using geometrical principles, his followers, the Pythagoreans, were able to prove that the sum of the angles of any regular-sided triangle is equal to that of two right angles (using the theory of parallels), and to solve any algebraic quadratic equations having real roots. They formulated the theory of proportion (ratio), which enhanced their knowledge of fractions, and used it in their study of harmonics upon their stringed instruments.             Quetelet, Lambert Adolphe Jacques (1796–1874) Belgian statistician. He developed tests for the validity of statistical information, and gathered and analyzed statistical data of many kinds. From his work on sociological data came the concept of the "average person."             Riemann, Georg Friedrich Bernhard (1826–1866) German mathematician whose system of non-Euclidean geometry, thought at the time to be a mere mathematical curiosity, was used by the physicist Albert Einstein to develop his general theory of relativity. Riemann made a breakthrough in conceptual understanding within several other areas of mathematics: the theory of functions, vector analysis, projective and differential geometry, and topology.

 

 

Page 56         He developed the Riemann surfaces to study complex function behavior. These multiconnected, many-sheeted surfaces can be dissected by crosscuts into a singly connected surface. By means of these surfaces he introduced topological considerations into the theory of functions of a complex variable, and into general analysis. He showed, for example, that all curves of the same class have the same Riemann surface. He also published a paper on hypergeometric series, invented "spherical" geometry as an extension of hyperbolic geometry, and in 1855–56 lectured on his theory of Abelian functions, one of his fundamental developments in mathematics.             Russell, Bertrand Arthur William, 3rd Earl Russell (1872–1970) British philosopher and mathematician who contributed to the development of modern mathematical logic. His works include Principia Mathematica (1910–13), with Alfred Whitehead, in which he attempted to show that mathematics could be reduced to a branch of logic.             Shannon, Claude Elwood (1916– ) U.S. mathematician who founded the science of information theory. He argued that entropy is equivalent to a shortage of information content (a degree of uncertainty), and obtained a quantitative measure of the amount of information in a given message. He reduced the notion of information to a series of yes/no choices, which could be presented by a binary code. Each choice, or piece of information, he called a "bit." In this way, complex information could be organized according to strict mathematical principles.             Viète, François (1540–1603) French mathematician who developed algebra and its notation. He was the first mathematician to use letters of the alphabet to denote both known and unknown quantities, and is credited with introducing the term "coefficient" into algebra. His mathematical achievements were the result of his interest in cosmology; for example, a table giving the values of six trigonometrical lines based on a method originally used by Egyptian astronomer Ptolemy. Viète was the first person to use the cosine law for plane triangles and he also published the law of tangents.             Whitehead, Alfred North (1861–1947) English philosopher and mathematician. In his "theory of organism," he attempted a synthesis of metaphysics and science. His works include Principia Mathematica (1910–13), with Bertrand Russell. Whitehead's research in mathematics involved a highly original attempt—incorporating the principles of logic—to create an extension of ordinary algebra to universal algebra (A Treatise of Universal Algebra (1898)), and a meticulous reexamination of the relativity theory of Albert Einstein.             Glossary             A             abacus ancient calculating device made up of a frame of parallel wires on which beads are strung. The method of calculating with a handful of stones on a "flat surface" (Latin abacus) was familiar to the Greeks and Romans, and used by earlier peoples, possibly even in ancient Babylon; it survives in the more sophisticated bead-frame form of the Russian schoty and the Japanese soroban. The abacus has been superseded by the electronic calculator.             absolute value or modulus value, or magnitude, of a number irrespective of its sign. The absolute value of a number n is written |n| (or sometimes as mod n), and is defined as the positive square root of n2. For example, the numbers –5 and 5 have the same absolute value:             acute angle angle between 0° and 90°; that is, an amount of turn that is less than a quarter of a circle.             algorithm procedure or series of steps that can be used to solve a problem.             arc section of a curved line or circle. A circle has three types of arc: a semicircle, which is exactly half of the circle; minor arcs, which are less than the semicircle; and major arcs, which are greater than the semicircle.             arc minute, arc second units for measuring small angles, used in geometry, surveying, map-making, and astronomy. An arc minute (symbol ') is one-sixtieth of a degree, and an arc second (symbol ") is one-sixtieth of an arc minute. Small distances in the sky, as between two close stars or the apparent width of a planet's disk, are expressed in minutes and seconds of arc.             arithmetic mean the average of a set of n numbers, obtained by adding the numbers and dividing by n. For example, the arithmetic mean of the set of 5 numbers 1, 3, 6, 8, and 12 is             arithmetic progression, or arithmetic sequence, sequence of numbers or terms that have a common difference between any one term and the next in the sequence. For example, 2, 7, 12, 17, 22, 27, . . . is an arithmetic sequence with a common difference of 5.             asymptote in coordinate geometry, a straight line that a curve approaches progressively more closely but never reaches. The x and y axes are asymptotes to the graph of xy = constant (a rectangular hyperbola).             average in statistics, a term used inexactly to indicate the typical member of a set of data. It usually refers to the arithmetic mean. The term is also used to refer to the middle member of the set when it is sorted in ascending or descending order (the median), and the most commonly occurring item of data (the mode), as in "the average family."             axiom statement that is assumed to be true and upon which theorems are proved by using logical deduction; for example, two straight lines cannot enclose a space. The Greek mathematician Euclid used a series of axioms that he considered could not be demonstrated in terms of simpler concepts to prove his geometrical theorems.             axis (plural axes) in geometry, one of the reference lines by which a point on a graph may be located. The horizontal

 

 

Page 57         axis is usually referred to as the x-axis, and the vertical axis as the y-axis. The term is also used to refer to the imaginary line about which an object may be said to be symmetrical (axis of symmetry)—for example, the diagonal of a square—or the line about which an object may revolve (axis of rotation).             B             binomial expression consisting of two terms, such as a + b or a–b.             C             cardinal number one of the series of numbers 0, 1, 2, 3, 4, . . . Cardinal numbers relate to quantity, whereas ordinal numbers (first, second, third, fourth, . . .) relate to order.             catastrophe theory mathematical theory developed by the French mathematician René Thom in 1972, in which he showed that the growth of an organism proceeds by a series of gradual changes that are triggered by, and in turn trigger, large-scale changes or "catastrophic" jumps. It also has applications in engineering—for example, the gradual strain on the structure of a bridge that can eventually result in a sudden collapse—and has been extended to economic and psychological events.             chance likelihood, or probability, of an event taking place, expressed as a fraction or percentage. For example, the chance that a tossed coin will land heads up is 50%.             circumference curved line that encloses a curved plane figure, for example a circle or an ellipse. Its length varies according to the nature of the curve, and may be ascertained by the appropriate formula. The circumference of a circle is pd or 2pr, where d is the diameter of the circle, r is its radius, and p is the constant pi, approximately equal to 3.1416.             concave polygon term used to describe any polygon that has an interior angle greater than 180°.             cone solid or surface consisting of the set of all straight lines passing through a fixed point (the vertex) and the points of a circle or ellipse whose plane does not contain the vertex.             congruent having the same shape and size, as applied to two-dimensional or solid figures. With plane congruent figures, one figure will fit on top of the other exactly, though this may first require rotation and/or rotation of one of the figures.             convex term used to describe any polygon possessing no interior angle greater than 180°.             coordinate number that defines the position of a point relative to a point or axis (reference line). Cartesian coordinates define a point by its perpendicular distances from two or more axes drawn through a fixed point mutually at right angles to each other. Polar coordinates define a point in a plane by its distance from a fixed point and direction from a fixed line.             correlation the degree of relationship between two sets of information. If one set of data increases at the same time as the other, the relationship is said to be positive or direct. If one set of data increases as the other decreases, the relationship is negative or inverse. Correlation can be shown by plotting a best-fit line on a scatter diagram.             cube regular solid figure whose faces are all squares. It has 6 equal-area faces and 12 equal-length edges.             cube to multiply a number by itself and then by itself again. For example, 5 cubed = 53 = 5 × 5 × 5 = 125. The term also refers to a number formed by cubing; for example, 1, 8, 27, 64 are the first four cubes.             D             degree unit (symbol °) of measurement of an angle or arc. A circle or complete rotation is divided into 360°. A degree may be subdivided into 60 minutes (symbol '), and each minute may be subdivided in turn into 60 seconds (symbol ").             digit any of the numbers from 0 to 9 in the decimal system. Different bases have different ranges of digits. For example, the hexadecimal system has digits 0 to 9 and A to F, whereas the binary system has two digits (or bits), 0 and 1.             dimension any directly measurable physical quantity such as mass (M), length (L), and time (T), and the derived units obtainable by multiplication or division from such quantities. For example, acceleration (the rate of change of velocity) has dimensions (LT–2), and is expressed in such units as km s–2. A quantity that is a ratio, such as relative density or humidity, is dimensionless.             E             equilateral of a geometrical figure, having all sides of equal length. For example, a square and rhombus are both equilateral four-sided figures. An equilateral triangle, to which the term is most often applied, has all three sides equal and all angles equal (at 60°).             F             Fibonacci numbers in their simplest form, a sequence in which each number is the sum of its two predecessors (1, 1, 2, 3, 5, 8, 13, . . .). They have unusual characteristics with possible applications in botany, psychology, and astronomy.             fractal irregular shape or surface produced by a procedure of repeated subdivision. Generated on a computer screen, fractals are used in creating models of geographical or biological processes (for example, the creation of a coastline by erosion or accretion, or the growth of plants).             G             golden section visually satisfying ratio, first constructed by the Greek mathematician Euclid and used in art and architecture. It is found by dividing a line AB at a point O such that the rectangle produced by the whole line and one of the segments is equal to the square drawn on the other segment. The ratio of the two segments is about 8:13 or 1:1.618, and a rectangle whose sides are in this ratio is called a golden rectangle. The ratio of consecutive Fibonacci numbers tends to the golden ratio.             I             infinity mathematical quantity that is larger than any fixed assignable quantity; symbol ¥. By convention, the result of dividing any number by zero is regarded as infinity.             M             Möbius strip structure made by giving a half twist to a flat strip of paper and joining the ends together. It has certain remarkable properties, arising from the fact that it has only one edge and one side. If cut down the center of the strip, instead of two new strips of paper, only one long strip is produced. It was discovered by the German mathematician August Möbius.             O             ordinal number one of the series first, second, third, fourth, . . . Ordinal numbers relate to order, whereas cardinal numbers (1, 2, 3, 4, . . .) relate to quantity, or count.

 

 

Page 58         P             parallel lines and parallel planes straight lines or planes that always remain a constant distance from one another no matter how far they are extended. This is a principle of Euclidean geometry. Some non-Euclidean geometries, such as elliptical and hyperbolic geometry, however, reject Euclid's parallel axiom.             perpendicular at a right angle; also, a line at right angles to another or to a plane. For a pair of skew lines (lines in three dimensions that do not meet), there is just one common perpendicular, which is at right angles to both lines; the nearest points on the two lines are the feet of this perpendicular.             polygon plane (two-dimensional) figure with three or more straight-line sides. Common polygons have names which define the number of sides (for example, triangle, quadrilateral, pentagon).             polyhedron solid figure with four or more plane faces. There are only five types of polyhedron (with all faces the same size and shape); they are the tetrahedron (four equilateral triangular faces), cube (six square faces), octahedron (eight equilateral triangles), dodecahedron (12 regular pentagons), and icosahedron (20 equilateral triangles).             progression sequence of numbers each occurring in a specific relationship to its predecessor. An arithmetic progression has numbers that increase or decrease by a common sum or difference (for example, 2, 4, 6, 8); a geometric progression has numbers each bearing a fixed ratio to its predecessor (for example, 3, 6, 12, 24); and a harmonic progression has numbers whose reciprocals are in arithmetical progression, for example 1, , , 1/4.             R             radian SI unit (symbol rad) of plane angles, an alternative unit to the degree. It is the angle at the center of a circle when the center is joined to the two ends of an arc (part of the circumference) equal in length to the radius of the circle. There are 2p (approximately 6.284) radians in a full circle (360°).             ratio measure of the relative size of two quantities or of two measurements (in similar units), expressed as a proportion. For example, the ratio of vowels to consonants in the alphabet is 5:21; the ratio of 500 m to 2 km is 500:2,000, or 1:4. Ratios are normally expressed as whole numbers, so 2:3.5 would become 4:7 (the ratio remains the same provided both numbers are multiplied or divided by the same number).             real number any of the rational numbers (which include the integers) or irrational numbers. Real numbers exclude imaginary numbers, found in complex numbers of the general form a + bi where i = Ö–1, although these do include a real component a.             rhombus equilateral parallelogram. Its diagonals bisect each other at right angles, and its area is half the product of the lengths of the two diagonals. A rhombus whose internal angles are 90° is called a square.             root of an equation, a value that satisfies the equality. For example, x = 0 and x = 5 are roots of the equation x2 –5x = 0.             S             symmetry exact likeness in shape about a given line (axis), point, or plane. A figure has symmetry if one half can be rotated and/or reflected onto the other. (Symmetry preserves length, angle, but not necessarily orientation.)             T             tangram puzzle made by cutting up a square into seven pieces.             tetrahedron (plural tetrahedra) solid figure (polyhedron) with four triangular faces; that is, a pyramid on a triangular base. A regular tetrahedron has equilateral triangles as its faces.             theorem mathematical proposition that can be deduced by logic from a set of axioms (basic facts that are taken to be true without proof). Advanced mathematics consists almost entirely of theorems and proofs, but even at a simple level theorems are important.             trapezoid in geometry, a four-sided plane figure (quadrilateral) with two of its sides parallel. If the parallel sides have lengths a and b and the perpendicular distance between them is h (the height of the trapezoid), its area A =  h(a + b).             Further Reading           Abbott, Percival, and Wardle, Michael Ernest Trigonometry (1991)           Anderson, Marlow First Course in Abstract Algebra: Rings, Groups and Fields (1995)           Ashurst, F. Gareth Founders of Modern Mathematics (1982)           Balz, A. G. Descartes and the Modern Mind (1952)           Barnsley, Michael F. Fractals Everywhere (1993)           Bell, R. J. T. Coordinate Geometry (1959)           Belsom, Chris Statistics (1997)           Berger, Marcel; Cole, Michael; and Levy, Silvio Geometry (1989)           Boyer, Carl B. A History of Mathematics (1968)           Brown, Stuart Leibniz (1984)           Butler, E. M. Heinrich Heine: A Biography (1956)           Casti, John L. Reality Rules (1992)           Chaitin, Gregory J. Algorithmic Information Theory (1987)           Chase, Warren, and Bown, Fred General Statistics (1997)           Cohen, Jack, and Stewart, lan The Collapse of Chaos (1993)           Coxeter, H. S. M. Introduction to Geometry (1969)           Crossley, J. N.; Ash, C. J.; Brickhill, C. J.; Stillwell, J. C.; and Williams, N. H. What Is Mathematical Logic? (1990)           Davidson, Hugh Blaise Pascal (1983)           Davis, Philip J., and Hersh, Reuben The Mathematical Experience (1981), Descartes' Dream (1986)

 

 

Page 59       Davis, Philip J., and Chinn, William G. 3.1416 and All That (1985)           Devlin, Keith Mathematics: The New Golden Age (1988), Logic and Information (1991), Mathematics, the Science of Patterns (1994)           Dijksterhuis, E. J. Archimedes (1956)           Dudley, Underwood A Budget of Trisections (1987)           Ekeland, Ivar Mathematics and the Unexpected (1988)           Field, Michael, and Golubitsky, Martin Symmetry in Chaos (1992)           Fraleigh, John B. A First Course in Abstract Algebra (1989)           Garfunkel, Solomon (ed.) For All Practical Purposes (1994)           Gauk, Roger Descartes: An Intellectual Biography (1995)           Goldstein, Larry Joel Algebra and Trigonometry and Their Applications (1996)           Gorman, Peter Pythagoras: A Life (1978)           Graham, Ronald L.; Knuth, Donald E.; and Patashnik, Oren Concrete Mathematics (1994)           Grattan-Guinness, l. Joseph Fourier (1972)           Greenberg, Martin Jay Euclidean and Non-Euclidean Geometries (1993)           Grene, Marjorie Descartes (1985)           Guillen, Michael Bridges to Infinity (1984)           Hansen, Vagn Lundsgaard Geometry in Nature (1993)           Harper, P. G., and Weaire, D. L. Introduction to Physical Mathematics (1985)           Jacobs, Harold R. Mathematics, a Human Endeavour (1994)           Jacobs, Konrad Invitation to Mathematics (1992)           Jesseph, Douglas M. Berkeley's Philosophy of Mathematics (1993)           Kaufmann, Jerome E. Trigonometry (1994)           Kitchens, Larry Exploring Statistics: A Modern Introduction to Data Analysis and Inference (1998)           Kitcher, Philip The Nature of Mathematical Knowledge (1984)           Kline, Morris Mathematics and the Search for Knowledge (1985)           Koosis, Donald J. Statistics: A Self-Teaching Guide (1997)           Kostrikin, A. I. Introduction to Algebra (1982)           Lavine, Shaughan Understanding the Infinite (1994)           Legendre, Adrien Marie; Brewster, David; and Carlyle, Thomas Elements of Geometry and Trigonometry: With Notes (1824)           Lewin, Roger Complexity (1992)           Livingston, Charles Knot Theory (1993)           McLeish, John Number (1991)           Maor, Eli The Story of a Number (1994), Trigonometric Delights (1998)           Mendelson, Elliott Introduction to Mathematical Logic (1964)           Menhard, J. Pascal: His Life and Works (1952)           Newmark, Joseph Statistics and Probability in Modern Life (1997)           O'Meara, Dominic Pythagoras Revived: Mathematics and Philosophy in Late Antiquity (1989)           Osserman, Robert Poetry of the Universe (1995)           Ore, Oystein, and Wilson, Robin James Graphs and Their Uses (1990)           Paulos, John Allen Innumeracy (1988), Beyond Numeracy (1991)           Peterson, Ivars The Mathematical Tourist (1988), Islands of Truth (1990)           Rosen, Kenneth H. Elementary Number Theory (1988)           Salem, Lionel; Testard, Frédéric; and Salem, Coralie The Most Beautiful Mathematical Formulas (1992)           Saw, Ruth Leibniz (1956)           Schroeder, Manfred Fractals, Chaos, Power Laws (1991)           Siegel, Andrew F., and Morgan, Charles J. Statistics and Data Analysis: An Introduction (1996)           Sigmund, Karl Games of Life (1993)           Smith, Geoff Introductory Mathematics: Algebra and Analysis (1998)           Stanley, Thomas Pythagoras (1989)           Stewart, lan Does God Play Dice? (1989), Galois Theory (1989), The Problems of Mathematics (1992), Nature's Numbers (1995), Concepts of Modern Mathematics (1995)           Sved, Marta Journey into Geometries (1991)           Tignol, Jean-Pierre Galois' Theory of Algebraic Equations (1988)           Weeks, Jeffrey R. The Shape of Space (1985)           Wells, David The Penguin Dictionary of Curious and Interesting Numbers (1986), You Are a Mathematician: a Wise and Witty Introduction to the Joy of Numbers (1998)