2.1 Introduction

Before diving into the recipes, we would like to step briefly through some basic set concepts and define the terminology used in this chapter. Although we are sure you are familiar with the mathematical concepts of sets, intersections, and unions, we would like to put each of these set-algebra terms into the context of a real-world example.

2.1.1 Components

There are three types of components to be aware of when working with sets. First is the set itself. A set is a collection of elements, and, for our purposes, an element is a row in a database table or a row returned by a query. Lastly, we have the universe, which is a term we use to refer to the set of all possible elements for a given set.

2.1.1.1 Sets

A set is a collection of elements. By definition, the elements must not be duplicated, and they are not ordered. Here, the mathematical definition of a set differs from its practical use in SQL. In the real world, it's often useful to sort the elements of a set into a specified order. Doing so allows you to find extremes such as the top five, or bottom five, records. Figure 2-1 shows an example of two sets. We'll be referring to these examples as we discuss various aspects of set terminology.

Figure 2-1. Two sets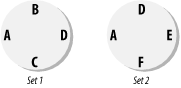

For our purposes, we will consider a set to be a collection of rows from a table identified by one common element. Consider, for example, the following table of order items. This table is a collection of sets, where each set is identified by a unique order-identification number.

CREATE TABLE OrderItems(
   OrderId INTEGER,
   ItemId INTEGER,
   ProductId CHAR(10),
   Qty INTEGER,
   PRIMARY KEY(OrderId,ItemId)
)

Each set in this case represents an order and will have a number of elements that are not duplicated. The elements will be rows defining the products and the quantity of those products being ordered. The common element is the OrderId column.

Sets and Primary Keys How does the primary key relate to the common element that defines a set? The answer is that they really don't need to be related at all. Any column, or combination of columns, in your table can be thought of as defining a set. It's really a matter of thinking about the data in a way that is useful to you. In the OrderItems table, the OrderId column is the common column that defines the set of all line items for an order. That's certainly a useful view of the data, but there are other ways to look at the data as well. The ProductId column, for example, defines the set of line items for a particular product. In real life, the sets you think about most are likely to correspond to your foreign-key columns. While more than one column can be used to define a set, it's highly unlikely for that list of columns to contain the table's primary key. If that were the case, each "set" would consist of only one record. If your sets only contain one record, you should probably reconsider your table structure or your interpretation of the sets in your table. Otherwise, you might run into trouble trying to apply the recipes shown in this chapter.

Using SQL, it is easy to list all elements from a set. You simply issue a SELECT statement with a WHERE clause that identifies the specific set of interest. The following query returns all line-item records in the set identified by order #112:

SELECT * FROM OrderItems WHERE OrderId=112

In this chapter, we will work with sets that are always in one table. Many authors try to demonstrate set operations using two different tables. This approach has two problems. First, while advantageous from a demonstration perspective, you will seldom find a database with two tables that both have the same structure. Second, there are many hidden possibilities for writing queries that come to light when you think of different sets as different slices of the same table. By focusing our recipes on a single table, we hope to open your mind to these possibilities.

2.1.1.2 Elements

An element is a member of a set. In Figure 2-1, each individual letter is an element. For our purposes, when working with SQL, an element is a row of a table. In SQL, it is often useful not to think of elements as unified entities. In the pure mathematical sense of the term, it's not possible to divide an element of a set into two or more components. In SQL, however, you can divide an element into components. A table is usually composed of many different columns, and you'll often write queries that operate on only a subset of those columns.

For example, let's say that you want to find the set of all orders that contain an explosive, regardless of the quantity. Your elements are the rows in the OrderItems table. You'll need to use the ProductId column to identify explosives, and you'll need to return the OrderId column to identify the orders, but you have no use for the other columns in the table. Here's the query:

SELECT OrderId 
FROM OrderItems o
GROUP BY OrderId
HAVING EXISTS( 
   SELECT * 
   FROM OrderItems o1 
   WHERE o1.ProductId='Explosive' AND o.OrderId=o1.OrderId)

This query actually uses one of the set operations that you'll read about in this chapter. The operation is known as the contains operation, and it corresponds to the SQL keyword EXISTS.

2.1.1.3 Universes

A universe is the set of all possible elements that can be part of a given set. Consider Sets 1 and 2 from Figure 2-1. Each set is composed of letters of the alphabet. If we decided that only letters could be set elements, the universe for the two sets would be the set of all letters as shown in Figure 2-2.

Figure 2-2. A possible universe for Sets 1 and 2

For a more real-life example of a set universe, assume that a school offers 40 possible courses to its students. Each student selects a small number of those 40 courses to take during a given semester. The courses are the elements. The courses that a given student is taking constitute a set. Different students are taking different combinations and numbers of courses. The sets are not all the same, nor are they all the same size, yet they all contain elements from the same universe. Each student must choose from among the same 40 possibilities.

In the student/course example just given, all elements of all sets come from the same universe. It's also possible for some sets in a table to have different universes than others. For example, assume that a table contains a list of finished case studies that students have presented. Further assume that the universe of possible case studies is different for each course. If you consider a set to be defined by a course and a student, the universe of elements that applies depends on the course that the student took. Each course will have a different universe.

2.1.2 Set Operations

Set operations allow you to take two sets and return some sort of meaningful result. The exact result depends on the operation being performed. For example, you can take two sets and return only those elements that appear in both sets. This operation is known as the intersection. Other operations include: contains, union, complement, and difference.

2.1.2.1 Contains

The contains operation tells you whether a specific element can be found within a set. Figure 2-3 shows that Set 1 (from Figure 2-1) contains the letter "D."

Figure 2-3. Set 1 contains a "D"

Contains is one of the very basic set-algebra operations and can be implemented directly in SQL by combining a SELECT statement with an EXISTS clause. For example, in the following query, EXISTS is used for each student in the StudentMaster table to see if that student is also in the set of students who have taken the course numbered ACCN101:

SELECT * FROM StudentMaster sm
WHERE EXISTS (SELECT * FROM Students s
              WHERE sm.StudentName = s.StudentName
                AND s.CourseId = 'ACCN101')

The use of EXISTS is so common that you might not even think much about the underlying set operation that it represents.

2.1.2.2 Intersection

An intersection is an operation where two or more sets are compared for common elements. For example, Figure 2-4 shows the intersection between sets 1 and 2.

Figure 2-4. Set 3 is the intersection of Sets 1 and 2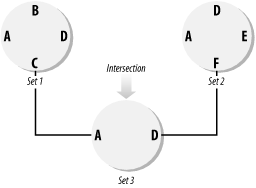

A typical question answered by an intersection is which students have taken ACCN101 who have also taken MGMT120. The SQL-92 standards specify the use of the keyword INTERSECT to implement the intersection operation. Thus, you should be able to write:

SELECT DISTINCT StudentName
FROM Students
WHERE CourseId='ACCN101'
INTERSECT
SELECT DISTINCT StudentName
FROM Students
WHERE CourseId='MGMT120'

Unfortunately, SQL Server does not implement the INTERSECT keyword. The intersection recipes in this chapter show some techniques for working around this limitation. In addition, this chapter shows you how to perform a partial intersection. A partial intersection allows you to find elements that belong to a specific number of sets, but not necessarily to all sets.

2.1.2.3 Union

A union is a way to combine two or more sets into one larger set, as shown in Figure 2-5. The resulting set contains all elements from both sets.

Figure 2-5. Set 4 is the union of Sets 1 and 2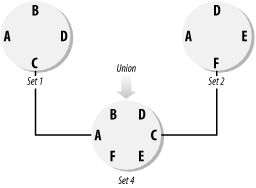

SQL (as a language) is well-equipped to work with unions and implements the union operation using the UNION keyword. This allows you to take the rows returned by two SELECT statements and blend them together into one result set. For example, the following query returns a list of students who have taken either ACCN101 or MGMT120:

SELECT * FROM Students
WHERE CourseId = 'ACCN101'
UNION
SELECT * FROM Students
WHERE CourseId = 'MGMT120'

In SQL, the UNION operation removes all duplicate rows from the result. With respect to this example, if a student has taken both courses, he will still only be listed once. If you want to preserve the duplicated rows, you can use UNION ALL in place of UNION.

When you execute a SELECT statement using the UNION operator, the server must execute each query separately. In many cases, unions can be achieved more efficiently without the UNION operator. One typical example is when you define a WHERE clause as a range that combines two or more set identifications. Another such case is when you are calculating aggregated information over several sets.

2.1.2.4 Complement

A complement is the set of all elements in a universe that are missing from a set. Figure 2-6 shows Set 1 and its complement with respect to the universe shown earlier in Figure 2-2.

Figure 2-6. A set and its complement

The complement operation is closely related to the universe of the set, and a union of both a complement and the original set gives you the universe for that set. As you'll later see in one of the recipes, an example of such an operation is to search a student's records and generate a list of missing term papers.

Do not be misled by the simplicity of this concept. Working with complements requires the definition of a universe. It is often possible to define a universe with a range; for example, you can define a particular container to have 100 possible slots. In such a case, it is fairly easy to operate with complements. However, if your problem requires that you specifically define every possible element for a set, the complexity of the complement operation will increase. In that case, you'll have to define a universe in a different table and join that table to your query.

2.1.2.5 Difference

The difference between two sets is the set of elements in one set that is not present in the other. Figure 2-7 illustrates the difference between Set 1 and Set 2.

Figure 2-7. The difference between two sets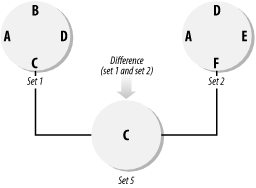

Set difference is a common problem when programming with sets, and it's useful when you want to find discrepancies between two or more sets. You can subtract one set from another, one set from all others, or many sets from one specific set.

The SQL-92 standard specifies that the EXCEPT keyword be used to implement the set-difference operation. Unfortunately, as with INTERSECTION, the EXCEPT keyword hasn't been implemented yet in SQL Server. In this chapter, we'll show you a different way to generate the difference between two sets.