|
|
|
8.1 Statistical ConceptsStatistics is an interesting branch of mathematics that is becoming more important in the business world. To fully understand the recipes in this chapter, you'll need to have some grasp of statistics. You also need to understand the language of statistics. In this section, we'll provide a brief introduction to some of the statistical terms that you'll see throughout this chapter. Then we'll explain — in non-SQL terms — the math behind the statistics generated by this chapter's recipes.
There are two types of data that can be manipulated with statistical tools: cross-sectional data and time-series data. Cross-sectional data is a snapshot that is collected at a single point in time. It has no time dimension. A typical example of cross-sectional data would be a set of height measurements of children of different ages. Computing the average of all the measurements for a given age gives you the average height of a child of that age. The specific date and time on which any given measurement was taken is irrelevant. All that matters is the height of each child and the child's age when that height was measured. The second type of data that you'll encounter is time-series data. With time-series data, every measurement has a time dimension associated with it. For example, you can look at stock-market prices over some period of time, and you'll find that the share price for any given company differs from day to day. And, not only from day to day, but also typically from hour to hour and minute to minute. A share price by itself means nothing. It's the share price coupled with the time at which that price was effective that is meaningful. A list of such prices and times over a given period is referred to as a time series. We need to define five more terms before proceeding into the sections that describe the calculations behind the various statistics discussed in this chapter. These terms are population, sample, sample size, case, and value. Consider the problem of having a large box of oranges for which you need to determine the sweetness level so that you can sell the box at the best possible price. That box of oranges represents your population. Now you could taste each orange in the box to check the sweetness level, but then you wouldn't have any oranges left to sell. Instead, you might choose to test only a few oranges — say, three. Those oranges that you test represent a sample, and the number of oranges in the sample represents the sample size. From a statistical point of view, you are testing a representative sample and then extrapolating the results to the oranges remaining in the box. Continuing with our example, each orange in a sample represents a specific case. For each case — or orange — you must test the sweetness level. The result of each test will be a value — usually a number — indicating how sweet the orange really is. Throughout this chapter, we use the term case to refer to a specific measurement in the sample. We use the term value to refer to a distinct numeric result. A value may occur more than once in a sample. For example, three oranges (three cases) may all have the same sweetness value. Now that you have a good grasp of the statistical terms used in this chapter, you can proceed to the following sections describing various statistical measurements and calculations. The calculations described in these upcoming sections form the basis for the recipes shown later in the chapter. 8.1.1 MeanA mean is a type of average, often referred to as an arithmetic average. Given a sample set of values, you calculate the mean by summing all the values and dividing the result by the sample size. Consider the following set of height values for seven kids in a hypothetical fifth-grade class:
Given these values, you compute the mean height by summing the values and dividing by the sample size of seven. For example: 100+100+100+110+115+120+180 = 825 cm 825 cm / 7 = 117.86 cm In this case, the mean height is 117.86 cm. As you can see, the mean height may not correspond to any student's actual height. 8.1.2 ModeA mode is another type of statistic that refers to the most frequently occurring value in a sample set. Look again at the numbers in the previous section on means. You'll see that the number of occurrences is as follows:
It's obvious that the most frequently occurring value is 100 cm. That value represents the mode for this sample set. 8.1.3 MedianA median is yet another type of statistic that you could loosely say refers to the middle value in a sample set. To be more precise, the median is the value in a sample set that has the same number of cases below it as above it. Consider again the following height data, which is repeated from the earlier section on means:
There are seven cases total. Look at the 110 cm value. There are three cases with values above 110 cm and three cases with values below 110 cm. The median height, therefore, is 110 cm. Computing a median with an odd number of cases is relatively straightforward. Having an even number of cases, though, makes the task of computing a median more complex. With an even number of cases, you simply can't pick just one value that has an equal number of cases above and below it. The following sample amply illustrates this point:
There is no "middle" value in this sample. 110 cm won't work because there are four cases having higher values and only three having lower values. 115 cm won't work for the opposite reason — there are three cases having values above and four cases having values below. In a situation like this, there are two approaches you can take. One solution is to take the lower of the two middle values as the median value. In this case, it would be 110 cm, and it would be referred to as a statistical median. Another solution is to take the mean of the two middle values. In this case, it would be 112.5 cm [(115 cm+110 cm)/2]. A median value computed by taking the mean of the two middle cases is often referred to as a financial median. It is actually possible to find an example where there is a median with an even number of cases. Such an example is: 1,2,3,3,4,5. There is an even number of cases in the sample; however, 3 has an equal number of cases above and below it, so that is the median. This example is exceptional, though, because the two middle cases have the same value. You can't depend on that occurring all the time. 8.1.4 Standard Deviation and VarianceStandard deviations and variance are very closely related. A standard deviation will tell you how evenly the values in a sample are distributed around the mean. The smaller the standard deviation, the more closely the values are condensed around the mean. The greater the standard deviation, the more values you will find at a distance from the mean. Consider again, the following values:
The standard deviation for the sample is calculated as follows:  Where:
Take the formula shown here for standard deviation, expand the summation for each of the cases in our sample, and you have the following calculation:  Work through the math, and you'll find that the calculation returns 28.56 as the sample's standard deviation. A variance is nothing more than the square of the standard deviation. In our example, the standard deviation is 28.56, so the variance is calculated as follows: 28.56 * 28.56 = 815.6736 If you look more closely at the formula for calculating standard deviation, you'll see that the variance is really an intermediate result in that calculation.
8.1.5 Standard ErrorA standard error is a measurement of a statistical projection's accuracy based on the sample size used to obtain that projection. Suppose that you were trying to calculate the average height of students in the fifth grade. You could randomly select seven children and calculate their average height. You could then use that average height as an approximation of the average height for the entire population of fifth graders. If you select a different set of seven children, your results will probably be slightly different. If you increase your sample size, the variation between samples should decrease, and your approximations should become more accurate. In general, the greater your sample size, the more accurate your approximation will be. You can use the sample size and the standard deviation to estimate the error of approximation in a statistical projection by computing the standard error of the mean. The formula to use is:  where:
We can use the data shown in the previous section on standard deviation in an example here showing how to compute the standard error. Recall that the sample size was seven elements and that the standard deviation was 28.56. The standard error, then, is calculated as follows:  Double the sample size to 14 elements, and you have the following:  A standard-error value by itself doesn't mean much. It only has meaning relative to other standard-error values computed for different sample sizes for the same population. In the examples shown here, the standard error is 10.78 for a sample size of 7 and 7.64 for a sample size of 14. A sample size of 14, then, yields a more accurate approximation than a sample size of 7. 8.1.6 Confidence IntervalsA confidence interval is an interval within which the mean of a population probably lies. As you've seen previously, every sample from the same population is likely to produce a slightly different mean. However, most of those means will lie in the vicinity of the population's mean. If you've computed a mean for a sample, you can compute a confidence interval based on the probability that your mean is also applicable to the population as a whole. 8.1.6.1 Creating the t-distribution tableConfidence intervals are a tool to estimate the range in which it is probable to find the mean of a population, relative to the mean of a current sample. Usually, in business, a 95% probability is all that is required. That's what we'll use for all the examples in this chapter. To compute confidence intervals in this chapter, we make use of a table called T_distribution. This is just a table that tells us how much we can "expand" the standard deviation around the mean to calculate the desired confidence interval. The amount by which the standard deviation can be expanded depends on the number of degrees of freedom in your sample. Our table, which you can create by executing the following SQL statements, contains the necessary t-distribution values for computing confidence intervals with a 95% probability: CREATE TABLE T_distribution( p DECIMAL(5,3), df INT ) INSERT INTO T_distribution VALUES(12.706,1) INSERT INTO T_distribution VALUES(4.303,2) INSERT INTO T_distribution VALUES(3.182,3) INSERT INTO T_distribution VALUES(2.776,4) INSERT INTO T_distribution VALUES(2.571,5) INSERT INTO T_distribution VALUES(2.447,6) INSERT INTO T_distribution VALUES(2.365,7) INSERT INTO T_distribution VALUES(2.306,8) INSERT INTO T_distribution VALUES(2.262,9) INSERT INTO T_distribution VALUES(2.228,10) INSERT INTO T_distribution VALUES(2.201,11) INSERT INTO T_distribution VALUES(2.179,12) INSERT INTO T_distribution VALUES(2.160,13) INSERT INTO T_distribution VALUES(2.145,14) INSERT INTO T_distribution VALUES(2.131,15) INSERT INTO T_distribution VALUES(2.120,16) INSERT INTO T_distribution VALUES(2.110,17) INSERT INTO T_distribution VALUES(2.101,18) INSERT INTO T_distribution VALUES(2.093,19) INSERT INTO T_distribution VALUES(2.086,20) INSERT INTO T_distribution VALUES(2.080,21) INSERT INTO T_distribution VALUES(2.074,22) INSERT INTO T_distribution VALUES(2.069,23) INSERT INTO T_distribution VALUES(2.064,24) INSERT INTO T_distribution VALUES(2.060,25) INSERT INTO T_distribution VALUES(2.056,26) INSERT INTO T_distribution VALUES(2.052,27) INSERT INTO T_distribution VALUES(2.048,28) INSERT INTO T_distribution VALUES(2.045,29) INSERT INTO T_distribution VALUES(2.042,30) INSERT INTO T_distribution VALUES(1.960,-1) The df column in the table represents a degrees of freedom value. The term degrees of freedom refers to a set of data items that can not be derived from each other. You need a value for degrees of freedom to select the appropriate p value from the table. The p column contains a coefficient that corrects the standard error around the mean according to the size of a sample. For calculating confidence intervals, use the number of cases decreased by 1 as your degrees of freedom. 8.1.6.2 Calculating the confidence intervalTo calculate the confidence interval for a sample, you first need to decide on a required probability. This will be the probability that the mean of the entire population falls within the confidence interval that you compute based on the mean of your sample. You also need to know the mean of your sample and the standard deviation from that sample. Once you have that information, calculate your confidence interval using the following formula:  where:
For example, consider the following data, which you also saw earlier in this chapter:
The mean of this data is 117.86, and the standard deviation is 28.56. There are 7 values in the sample, which gives 6 degrees of freedom. The following query, then, yields the corresponding t-distribution value: SELECT p FROM T_distribution WHERE df=6 p ------- 2.447 The value for P, which is our t-distribution value, is 2.447. The confidence interval, then, is derived as follows:   8.1.7 CorrelationA correlation coefficient is a measure of the linear relationship between two samples. It is expressed as a number between -1 to 1, and it tells you the degree to which the two samples are related. A correlation coefficient of zero means that the two samples are not related at all. A correlation coefficient of 1 means that the two samples are fully correlated — every change in the first sample is reflected in the second sample as well. If the correlation coefficient is -1, it means that for every change in the first sample, you can observe the exact opposite change in the second sample. Values in between these extremes indicate varying degrees of correlation. A coefficient of 0.5, for example, indicates a weaker relationship between samples than does a coefficient of 1.0. The correlation coefficient for two samples can be calculated using the following formula:  where:
Consider the two samples shown in Table 8-1. The first sample represents daily closing stock prices for a particular stock. The second sample represents the value of the corresponding stock-market index over the same set of days. An investor looking at this data might wonder how closely the index tracks the stock price. If the index goes up on any given day, is the stock price likely to go up as well? The correlation coefficient can be used to answer that question.
To compute the correlation coefficient of the stock price with respect to the index value, you can take the values shown in Table 8-1 and plug them into the formula shown earlier in this section. It doesn't matter which is X and which is Y. For this example, let X represent the stock price, and Y will represent the index value. The resulting calculation is as follows: 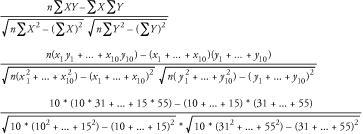 If you put the numbers into the formula, where stock prices represent the X series, index numbers represent the Y series, and number of samples is 10, you get the correlation coefficient of 0.40. The result tells us that the stock price is weakly correlated with the market index. The formula shown here looks scary at first, and it does take a lot of tedious work to compute a correlation by hand; however, you'll see that its implementation in SQL is quite straightforward. 8.1.8 AutocorrelationAutocorrelation is an interesting concept and is very useful in attempting to observe patterns in time-series data. The idea is to calculate a number of correlations between an observed time series and the same time series lagged by one or more steps. Each lag results in a different correlation. The end result is a list of correlations (usually around fifteen), which can be analyzed to see whether the time series has a pattern in it. Table 8-2 contains the index values that you saw earlier in Table 8-1. It also shows the autocorrelation values that result from a lag of 1, 2, and 3 days. When calculating the first correlation coefficient, the original set of index values is correlated to the same set of values lagged by one day. For the second coefficient, the original set of index values is correlated to the index values lagged by 2 days. The third coefficient is the result of correlating the original set of index values with a 3-day lag.
Please note that it's only possible to calculate a correlation coefficient between two equally sized samples. Therefore, you can use only rows 2 through 9 of Lag 1 when calculating the first correlation coefficient, rows 3 through 10 of Lag 2 for the second, and rows 4 through 11 of the Lag 3 for the third. In real life, you would likely have enough historical data to always use rows 1 through 9. You can see that the correlation coefficients of the first few lags are declining rather sharply. This is an indication that the time series has a trend (i.e., the values are consistently rising or falling). As you can see, the values of the first three autocorrelations in our example are declining. The first correlation is the strongest; therefore, the neighboring cases are related significantly. Cases that are 2 and 3 lags apart are still correlated, but not as strongly as the closest cases. In other words, the behavior of neighboring lags is related proportionally to the distance they are apart from each other. If two consecutive cases are increasing, it is probable that the third one will increase as well. The series has a trend. A decreasing autocorrelation is an indicator of a trend, but it has nothing to do with the direction of the trend. Regardless of whether the trend is increasing or decreasing, autocorrelation is still strongest for the closest cases (Lag 1) and weakest for the more distant lags. A sharp increase in the correlation coefficient at regular intervals indicates a cyclical pattern in your data. For example, if you were looking at monthly sales for a toy store, it is likely that every 12th lag you would observe a strong increase in the correlation coefficient due the Christmas holiday sales. In one of the recipes we show later in this chapter, you'll see how autocorrelation can be implemented in SQL. In addition, you'll see how SQL can be used to generate a crude graph of the autocorrelation results quickly. 8.1.9 Moving AveragesA moving average is used when some kind of smoothing is needed on a set of time-series data. To compute a moving average, you combine every value in the series with some number of preceding values and then compute the average of those values. The result is a series of averages giving a smoother representation of the same data, though some accuracy will be lost because of the smoothing.
Moving averages are commonly used in the financial industry to smooth out daily oscillations in the market price of a stock or other security. Table 8-3 shows a moving average for a stock price over a 10-day period. The left-hand column shows the daily stock price, while the right-hand column shows a 5-day moving average of that price. During the first four days, no moving average is possible, because a 5-day moving average requires values from 5 different days. Thus, the average begins on Day 5.
You can readily see that the 5-day moving average values in Table 8-3 smooth out most of the wild oscillations in the day-to-day price of the stock. The moving average also makes the very slight upward trend much more clear. Figure 8-1 shows a graph of this same data. Figure 8-1. A stock price and its 5-day moving average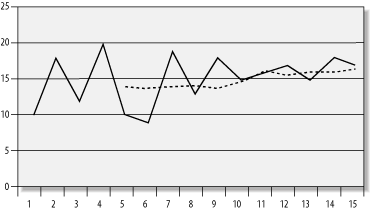 There are a number of different moving averages possible. A simple moving average, such as the one just shown in Table 8-3, represents the mean over a period for every case in the data set. All cases in the period are summed together, and the result is then divided by the number of cases in the period. It is possible, however, to extend the concept of a moving average further. For example, a simple exponential average uses just two values: the current value and the one before it, but different weights are attached to each of them. A 90% exponential smoothing would take 10% of each value, 90% of each preceding value (from the previous period), and sum the two results together. The list of sums then becomes the exponential average. For example, with respect to Table 8-3, an exponential average for Day 2 could be computed as follows: (Day 2 * 10%) + (Day 1 * 90%) = (18 * 10%) + (10 * 90%) = 1.8 + 9 = 10.8 Another interesting type of moving average is the weighted average, where the values from different periods have different weights assigned to them. These weighted values are then used to compute a moving average. Usually, the more distant a value is from the current value, the less it is weighted. For example, the following calculation yields a 5-day weighted average for Day 5 from Table 8-3. (Period 5 * 35%) + (Period 4 * 25%) + (Period 3 * 20%) + (Period 2 * 15%) + (Period 1 * 5%) = (10 * 35%) + (20 * 25%) + (12 * 20%) + (18 * 15%) + (10 * 5%) = 3.5 + 5 + 2.4 + 2.7+ 0.5 = 14.1 As you can readily see, a weighted moving average would tend to favor more recent cases over the older ones. |
|
|
|
is the summation operator. It's used as a shorthand way of telling you to add up all the values in a sample set. When you see 
symbol is the square-root operator. When you
see 
, you need to find the value that, when multiplied by itself, yields n. For example, 
is 3, because 3 * 3 = 9. Most calculators allow you to easily compute square roots. Another way to express 3 * 3, by the way, is to write it as 32. The small, raised 2 indicates that you should multiply the value by itself.
