2.6 Talking RDF: Lingo and Vocabulary

Right at this moment, you have enough understanding of the RDF graph to progress into the RDF/XML syntax in the next chapter. However, if you follow any of the conversations related to RDF, some terms and concepts might cause confusion. Before ending this chapter on the RDF graph, I thought I would spend some time on these potentially confusing concepts.

2.6.1 Graphs and Subgraphs

In any RDF graph, a subgraph of the graph would be a subset of the triples contained in the graph. As I said earlier, each triple is uniquely its own RDF graph, in its own right, and can actually be modeled within a separate directed graph. In Figure 2-3, the triple represented by the following is a subgraph of the entire set of N-Triples representing the entire graph:

<http://burningbird.net/articles/monsters3.htm> <http://burningbird.net/postcon/
elements/1.0/title> "Architeuthis Dux"

Taking this concept further, a union of two or more RDF graphs is a new graph, which the Model document calls a merge of the graphs. For instance, Figure 2-4 shows one graph containing exactly one RDF triple (one statement).

Figure 2-4. RDF graph with exactly one triple

Adding the following triple results in a new merged graph, as shown previously in Figure 2-3. Since both triples share the same subject, as determined by the URI, the mergence of the two attaches the two different triples to the same subject:

<http://burningbird.net/articles/monsters3.htm> <http://burningbird.net/postcon/elements/1.0/author> "Shelley Powers"

Now, if the subjects differed, the merged graph would still be valid—there is no rule or regulation within the RDF graph that insists that all nodes be somehow connected with one another. All the RDF graph insists on is that the triples are valid and that the RDF used with each is valid. Figure 2-5 shows an RDF graph of two merged graphs that have disconnected nodes.

Figure 2-5. Merged RDF graph with disconnected nodes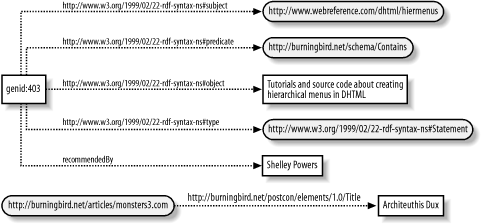

Blank nodes are never merged in a graph because there is no way of determining whether two nodes are the same—one can't assume similarity because of artificially generated identifiers. The only components that are merged are urirefs and literals (because two literals that are syntactically the same can be assumed to be the same). In fact, when tools are given two graphs to merge and each graph contains blank nodes, each blank node is given a unique identifier in order to separate it from the others before the mergence.

2.6.2 Ground and Not Graph

An RDF graph is considered grounded if there are no blank nodes. Figure 2-4 is an example of a grounded RDF graph, while Figure 2-5 is not because of the blank node (labeled genid:403). Additionally, an instance of an RDF graph is a graph in which each blank node has been replaced by an identifier, becoming a named node. In Figure 2-5, a named node replaced the blank node; if I were to run the RDF Validator against the RDF/XML that generated this example I would get a second instance, and the names used for the blank nodes would differ. Semantically the two graphs would represent the same RDF graph but are considered separate instances of the graph.

Finally, an RDF vocabulary is the collection of all urirefs from a specific RDF graph. Much discussion is made of the Dublin Core vocabulary or the RSS vocabulary and so on (discussed more in Chapter 6). However, a true RDF vocabulary can differ from an official implementation of it by the very fact that the urirefs may differ between the two.

Since this is a bit confusing, for the rest of the book when I refer to an RDF vocabulary, I'm referring to a schema of a particular vocabulary, rather than any one particular implementation or document derived from it.

2.6.3 Entailment

Within the RDF Semantics document, entailment describes two graphs, which are equal in all aspects. By this I mean that every assertion made about one RDF graph can be made with equal truth about the other graph. For instance, statements made in one graph are implicitly made in the other; if you believe the statement in the first, you must, through entailment, believe the same statement in the other.

As examples of entailment, the formal term subgraph lemma states that a graph entails all of its subgraphs, because whatever assertions can be made about the whole graph can also be made against the subgraphs, aside from differences associated with the subgraphing process (e.g., the original graph had two statements, while the subgraph had only one). Another lemma, instance lemma, states that all instances of a graph are entailed by the graph—instance in this case an implementation of a graph in which all blank nodes have been replaced by a literal or a uriref.

Earlier I talked about merging graphs. The merging lemma states that the merged graph entails all the graphs that form its final construction. Another lemma, monotonicity lemma, states that if a subgraph of a graph entails another graph, then the original graph also entails that second graph.

Within web specifications, one hopes not to run into terms such as lemma, which means "subsidiary proposition assumed to be valid and used to demonstrate a principal proposition," according to the dictionary. However, I know that the main purpose of the Semantics document within the RDF specification is to provide fairly concrete interpretations of the RDF graph theory so that implementers of the technology can provide consistent implementations. For those who primarily use RDF/XML technology rather than create parsers or RDF databases, an understanding of the pure RDF semantics isn't essential—but it is helpful, which is why I'm covering it, however lightly.

The interpolation lemma actually goes more into the true nature of entailment than the others, and so I'll cover it in more detail.

The interpolation lemma states:

S entails a graph E if and only if a subgraph of the merge of S is an instance of E.

This lemma basically states that you can tell whether one set of graphs entails another if you take a subgraph of the mergence of the graphs, replace the named nodes with blank nodes, and, if the result is an instance of the second set of graphs, the first set is said to entail them. From an editor's draft:

"To tell whether a set of RDF graphs entails another, check that there is some instance of the entailed graph which is a subset of the merge of the original set of graphs."

Oversimplification aside, what's important to realize about entailment is that it's not the same thing as equality. Equality is basically two graphs that are identical, even down to the same named nodes. Entailment implies something a little more sophisticated—that the semantics of an RDF construct as shown in a specific implementation of a graph map to that which is defined within the formal semantics of the model theoretic viewpoint of the abstract RDF graph. The information in the entailed graph is the same as the information in the other but may have a different physical representation. It is entailment that allows us to construct a graph using a node-edge-node pattern and know that this instance of the RDF graph is a valid one, and that whatever semantic constraints exist within the model theoretic viewpoint of RDF also exist within this real-world instance of RDF. Additionally, entailment allows different manipulations of the data in the graphs, as long as the original information is preserved.