12.1 Cryptography Explained

The most common way to describe cryptographic systems is to assume that one person (usually named Alice) wants to send a message to another person (Bob). However, a third person (Eve) is determined to eavesdrop on their conversation. Figure 12-1 shows the relationship between Alice, Bob, and Eve.

Figure 12-1. Alice, Bob, and Eve are commonly used to illustrate cryptography.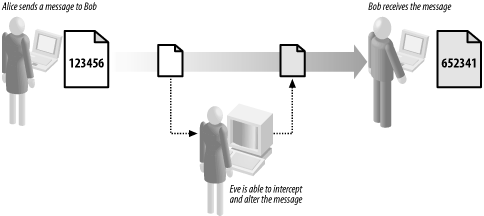

Let's assume that Eve will intercept and alter messages between Alice and Bob irrespective of how those messages are composed and sent. Although this might seem paranoid, there are benefits to this way of thinking. By assuming that Eve can intercept each message, you are, in effect, forced to regard the communications channel as insecure—this is a realistic approach because communications techniques that seem secure today may be compromised in the future. By assuming that Eve can read any message, we focus on the security of the message itself.

Cryptography has a long history, and different techniques for protecting messages have been in use for thousands of years. For most of that time, Alice, Bob, and Eve have represented real people or organizations. With advances in technology, cryptography has become irrevocably bound to the world of computers. Computers have facilitated stronger cryptographic techniques but also allowed people like Eve to mount stronger attacks on cryptography. Although we find it useful to talk about Alice, Bob, and Eve, these names are often a metaphor for computers.

When we say "Alice sends a message to Bob," we do not consider the details of how she does this, and as a result, we will be discussing techniques that are applicable in many different situations. For example, Alice may use her email client to compose and send a message, or she may have written an application that will communicate automatically with her bank to pay her bills while she is on vacation. Irrespective of how Alice communicates with Bob, her need for cryptography can be broken down into the three categories that we discuss in Section 12.1.1, Section 12.1.2, and Section 12.1.3.

12.1.1 Confidentiality

Confidentiality becomes an issue when Alice wants to send a message containing a secret to Bob. We assume that Eve can intercept and read the message, and that Alice and Bob do not want Eve to know the secret contained in the message.

The cryptographic solution to this problem is to obscure the contents of the message using encryption. Encryption ensures that Eve cannot understand the messages sent between Alice and Bob, even though she is able to intercept them. Figure 12-2 illustrates the role of encryption in confidentiality.

Figure 12-2. Alice uses encryption to ensure that her messages to Bob remain confidential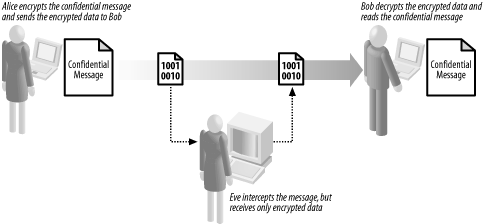

Encryption works on the basis that there is one piece of information that Eve has not been able to acquire, known as the key. The key is used as part of the encryption process and is kept secret. Alice selects an encryption algorithm and uses the secret key to create the encrypted data, as shown in Figure 12-3. When Bob receives the encrypted text, he uses the secret key to restore the confidential message so that he can read it.

Figure 12-3. Alice uses the confidential message and the secret key to create the encrypted data.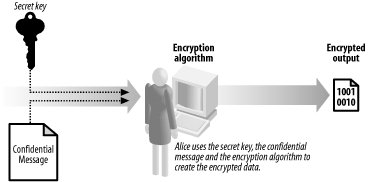

Using encryption changes the nature of the confidentiality problem—Alice and Bob can exchange confidential messages as long as Eve does not acquire the secret key. When Alice and Bob exchange messages, they send the encrypted data only—they never send the key, because they know that Eve can intercept it and then read their messages.

This is the very essence of encryption—Alice uses one secret that Eve does not know (the key) to protect another (the confidential message). However, Eve can read the confidential messages if she discovers or guesses the key.

In practice, using encryption becomes centered on protecting and managing these secret keys. Some types of encryption require Alice and Bob to know the key and are called symmetric encryption (because Alice and Bob have the same knowledge). The problem with symmetric encryption is that Alice and Bob need to agree on what the secret key will be before sending any messages.

Another approach is to use asymmetric encryption, where only Bob has to keep a secret. Bob creates a special pair of keys, one of which he keeps secret (known as the private key) and one that is given out to anyone who wants to send him a message (the public key). Bob can send Alice his public key openly, because he does not care if Eve intercepts it.

When Alice wants to send Bob a confidential message, she uses an asymmetric encryption technique to encrypt the data. This is similar to the model shown in Figure 12-3; but instead of using the secret key, Alice uses Bob's public key and the contents of the message as inputs.

When Bob receives the message, he decrypts it using his private key (which he always keeps secret) and restores the confidential message from the encrypted data. Eve cannot read the message unless she acquires Bob's secret key. Using this technique, Alice and Bob do not have to agree on a key that they both know, further reducing the chances that Eve can acquire the key during the agreement process. The use of asymmetrical encryption is also known as public key cryptography.

We discuss the .NET Framework's support for symmetric encryption in Chapter 14, and provide more information about public key cryptography in Chapter 15 and Chapter 16.

12.1.2 Integrity

Integrity becomes an issue when Alice wants to send a message to Bob but is concerned that Eve will tamper with the message and change the contents. In this case, Alice does not care if Eve can read the message—she only wants to make sure that Bob can detect any changes made by Eve.

Alice takes the message that she has written and creates a cryptographic hash code, which is a numeric code based on the contents of the message that acts as a "fingerprint" to identify the message. Changing even the smallest portion of the message results in a different hash code. Alice sends the message and the hash code to Bob.

Bob takes the message that he has received and creates his own hash code using the same technique that Alice used. If his code matches the one that Alice sent, Bob can assume that Eve has not modified the message—if the hash codes do not match, then Bob can assume that Eve has altered the message en route. Figure 12-4 illustrates the use of hash codes.

Figure 12-4. Alice and Bob use hash codes to check the integrity of their messages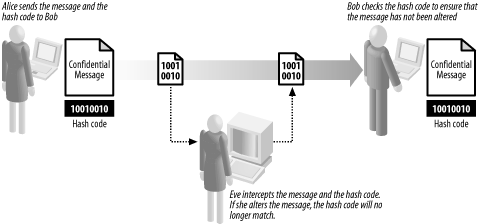

Eve will be able to change the message without detection if she changes the hash code as well. Eve creates a new message and a new hash code, both of which she sends to Bob. When Bob creates a hash code for the message, it will match the hash code he has received, leading him to think that the message has not been tampered with.

The solution to this problem is to use a "keyed" hash code, which uses the contents of the message and a secret key to create the hash code, as illustrated in Figure 12-5. Eve can still modify the message, but she can no longer create a valid hash code, because she lacks the key used to create the original code.

Figure 12-5. Keyed hash codes are created using the contents of the message and a secret key.

Unless Eve is able to discover the key, she will be unable to create hash codes that will fool Bob; if Eve acquires the key, she will be able to generate valid hash codes for her own messages, rendering Alice and Bob's efforts to ensure message integrity useless. As with confidentiality, the issue of integrity becomes one of protecting secret keys from Eve. We discuss the .NET Framework support for cryptographic hash codes in Chapter 13.

12.1.3 Authentication

The goal of authentication is to allow Bob to establish that Alice is the author of a message. For our purposes, this means that Alice should be able to create a "digital signature" for the message and that Bob should be able to check the signature to ensure that it is valid. In addition, Eve should not be able to create and sign messages as though she were Alice.

Digital signatures rely on asymmetric encryption techniques, although they are applied differently than we discussed earlier. Alice creates a pair of keys, one of which she makes public and one of which she keeps private. To sign the message, Alice creates a cryptographic hash code of the message that she wants to send to Bob, as discussed earlier. Alice then signs the hash code using her private key, as shown in Figure 12-6. This creates a digital signature that is unique to the combination of the document and Alice's private key.

Figure 12-6. Alice uses public key cryptography to create a digital signature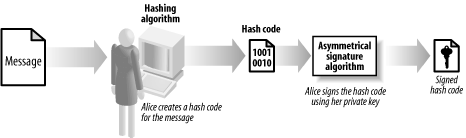

When Bob receives the message, he verifies the signature using Alice's public key. If the signature is valid, then Alice has "signed" the message, and Bob can assume that Eve has not forged the message.

Because digitally signing a document requires the creation of a hash code, it also addresses the issue of integrity that we discussed earlier. If Eve modifies the message that Alice has sent, then Alice's signature will not be valid. Bob will generate his own hash code for the message, and it will not be the same as the one Alice signed. Figure 12-7 shows the protocol for message signatures.

Figure 12-7. Alice uses a digital signature to authenticate a message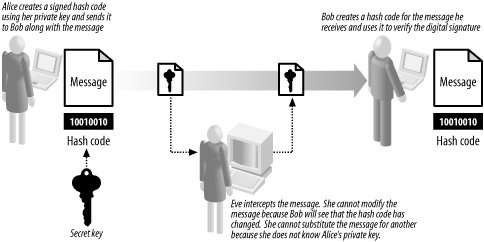

Eve is unable to forge messages from Alice, because she does not know Alice's secret key and is unable to create digital signatures that will fool Bob. However, as with the areas of confidentiality and integrity, if Eve is able to acquire the secret key, she will be able to sign messages as though she were Alice.